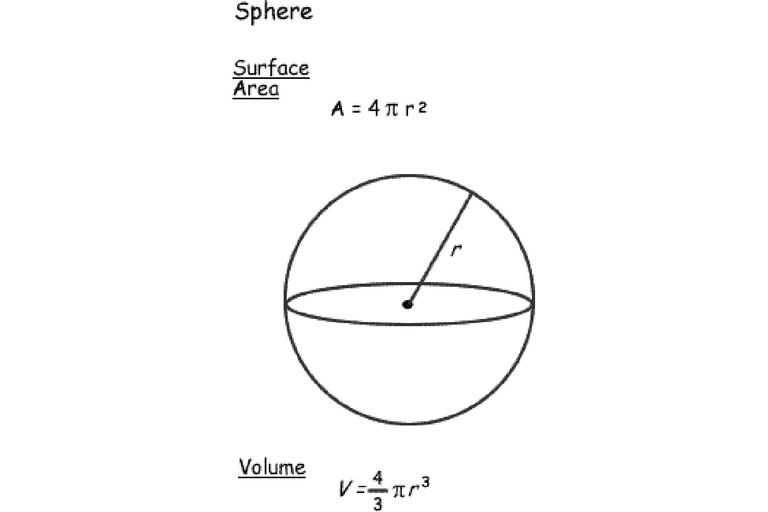
S=4πR²或者S=πd²或者S=4πR^2 上式中,r或R是球体的半径,d是球体的直径,π是圆周率,d=2R。 拓展资料 利球体表面积是指球面所围成的几何体的面积,它包括球面和球面所围成的空间用周长公式计算球的表面积。 球体表面積公式 球体表面積公式(球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。 球の体積 は、 身の上に心配あるので、参上。 球の表面積は、心配ある事情。 表面積$$球体の体積公式=\\frac{4πr^3}{3}$$ この球体の体積公式が覚えられない! という生徒のために覚え方を教えましょう! といっても割りと有名なやつなんだけどね。 身の上に心配あるさ~ 身=3 の上に=分子のこと 心=4 配=π
球的表面积公式 球的表面积公式画法
球体面積 公式
球体面積 公式-S:球の表面積ってどうやって求めるのだろう。 s:円の場合は細かな三角形に分割して面積を求めたよ。 円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。 s:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。 球的表面积计算公式 球的表面积=4πr^2, r为球半径 。 一个半圆绕直径所在直线旋转一周所成的空间几何体叫做球体,简称球,半圆的半径即是球的半径。球体是有且只有一个连续曲面的立体图形,这个连续曲面叫球面。 利用周长公式计算球的表面积 √表示根号




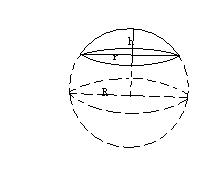
球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科
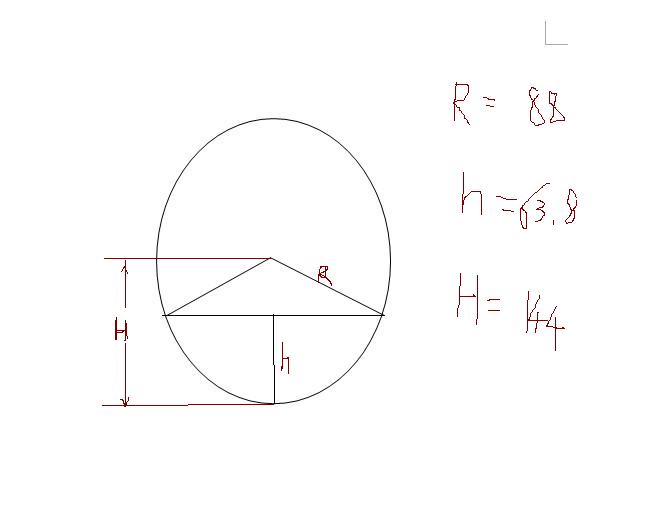
半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め 球体 面積 体積 公式ぐー477" ④ 球の体積 半径が7の球の体積をしとすると, リーまァが ー 考え方と解き方 面積と体積を求める公式にあてはめて 面積 4ァ x6=144z(cmう) *積 芋zx6'=2z(om 3 國 表面積 144zcm 体積 2rem 球の表面積はその球がちょ うと人 る円柱の側面積 球の体積の求め方(公式)の次は、球の表面積の求め方(公式)を学習しましょう。 下の図のように、 半径rの球があるとき、球の表面積は、4πr2となります。 これもまた、球の表面積の公式がなぜ4πr 2 となるのか疑問に思う人もいるでしょう。
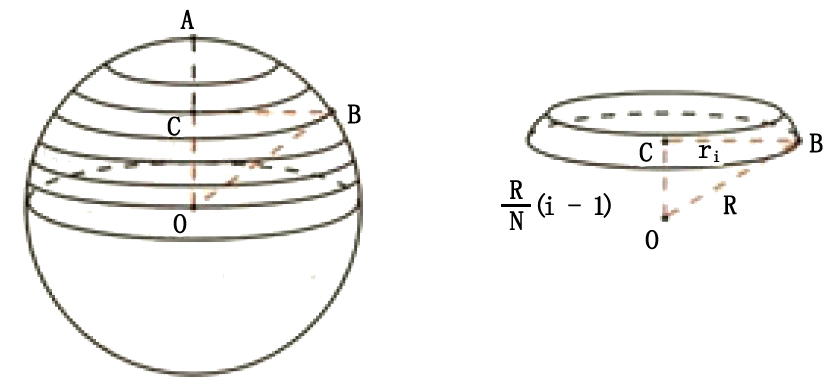
球冠表面积公式推导过程 编辑 语音 假定球冠最大开口部分圆的半径为 r ,对应球半径 R 有关系:r = Rcosθ,则有球冠积分表达: 球冠面积 微分 元 dS = 2πr×Rdθ = 2πR 2 ×cosθ dθ 积分下限为θ,上限π/2 所以:S = 2πR×R (1 sinθ) 其中:R (1 sinθ)即为球冠的自身①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r則由勾股弦定理知: a 2 =r 2h 2 = 小牟合方蓋截面面積。 (4)設其餘三部份截面面積為 S ,則 S= r 2a 2 = r 2(r 2h 2)h 2 ;也就是說,不管在何處截面, S=h 2 恆成立。 (5)接下來,取一個倒立的方錐,其邊長和高都等於 r ,則在高為 h 的地方截之,其截面面積亦為 h 2 。
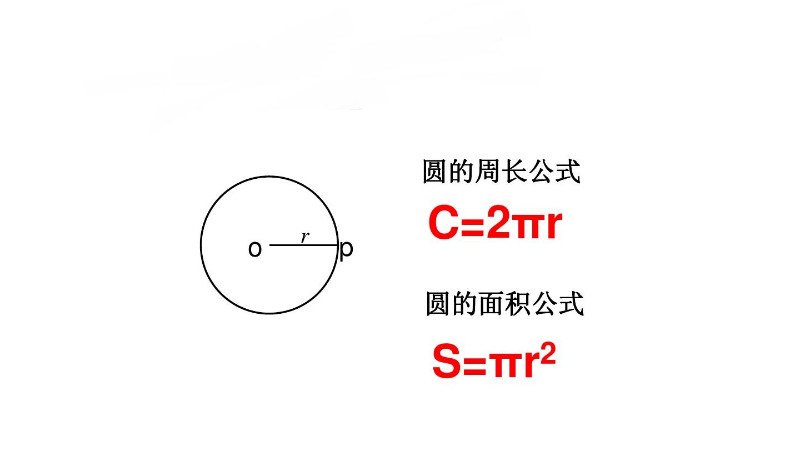
例えば、半径が12糎の円の面積は S=π×12 2 =144π(平方糎) となる。 次に、円周の長さは L=2πr である。 例えば、半径が6糎の円の円周は となる。 では、円ではなく球体の体積の公式はどうなるのか? 其れは、以下の公式である。 V=4/3×πr 3 である。 円の面積の公式 $\pi ab$ もちろん(1A)の方法で計算することもできますが、面倒なので(1C)の方法を駆使して楕円の面積を求めたいと思います。 まず、楕円体のまま体積を計算するのはめんどうなので、楕円体を球体に変換してやりましょう。關於球體體積計算器 球體體積計算器用於幫助您查找球體的體積。 球體積公式 以下是球體積的計算公式:




球冠面积 Stereohomology Csdn博客 球冠面积




3种方法来计算球体的半径
年の最高 球体 表面積 公式 球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和 球体表面积公式 怎样计算球体14/1/ 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立て球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 エクセルで球の表面積を計算する方法 エクセルで球の表面積を計算する前に、まずその定義について考えていきましょう。 実は級の表面積はその球の半径をrcmとすると、円周率π(パイ:314)を用いると、 表面積=4πr^2cm^2と表現することができます。




ベスト 球体積公式 犬イラスト



球的表面积公式 球的表面积公式画法
球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 \begin{equation} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation} となるので、確かに球冠の面積の公式で求めた結果と一致しています。 では、こちらも証明に入っていきます。 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するための複雑な公式であっても、その場で思い出すことができますね! 私は今でも語呂合わせで思い出すことがありますw あ! 語呂合わせで公式は覚えたけど どっちが体積で、どっちが表面積だっけ? というようにごちゃごちゃになっちゃう人も多いです。




圆锥与球与圆柱



微积分下的不规则图形的体积计算原理 科学探索
球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。球の表面積は 4×円周率×半径×半径=表面積 で求めることができます。 円周率をπ、半径をr、表面積をSとすると、 S=4πr 2 となります。 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: 4 3 π r 3




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org



1 球体计算公式2 球缺计算公式 尚书坊
球欠,球台の体積と球冠,球帯の表面積 レベル ★ マニアック 積分 更新日時 球を平面で切り取った立体の体積,および側面の面積の求め方を解説します。 結果を覚える必要はありませんが,導出方法はマスターしておきましょう。 目次 球を 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1 2πr × 1 2πr × π = π2 4 πr2★ 数学公式集 図形・面積・体積 For example 扇・弓・円・楕円・円錐・三角錐・角錐・球体・楕円体・台形・三角形・ など ・・
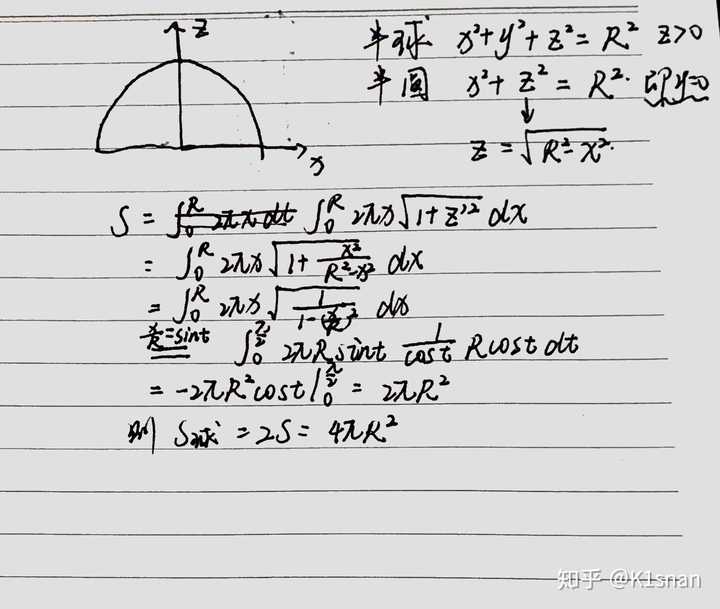



为何对圆周长公式积分无法得到球表面积公式 知乎




扇形面积公式计算公式 搜狗图片搜索
(円の面積) = π r 2 という公式が作られる。 円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。などについて論じている。佐伯(13)は,円の面積 公式を導く算数教科書の記述の背景にある,高校数学 の内容について論じている(pp5460)。 また,円の面積公式や球の体積公式の導出に関して, 現在までに幾つかの実践研究が行われている。例えば,球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半




数学趣谈 球面积公式的不同导出方法 参考网



球体表面积公式球体表面积球体表面积 公式证明 爱华网
一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin




扇形面积公式弧度制极坐标三种3个推导过程 计算机器在线计算



球体体积公式是球体体积公式是什么




球體表面積及體積的推導 每日頭條




用感覺理解球體表面積公式 Youtube



球体积的前世今生 科普中国



高中数学牛x 公式 利用三棱锥内切球的半径与体积关系式快速解题 努力学习网
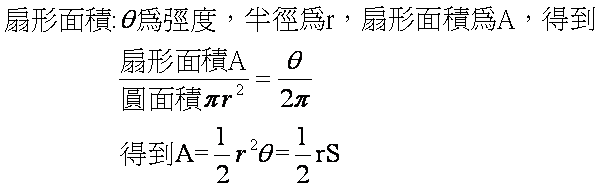



扇形的弧長與面積



Q Tbn And9gcrb4blzi9vddmsv6c33dfu2ymwljv9pqvinxvz2heat Qlxblsn Usqp Cau



球冠表面积计算公式 圣恩灵修网
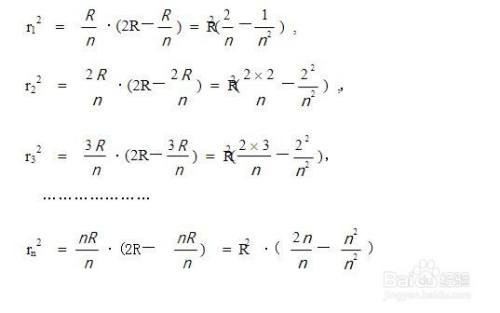



球体体积公式推导图解 百度经验




百科知识 小街网



1



球的面积公式是什么 扒拉扒拉



球的体积公式和表面积公式 中国练字网




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



球的面积公式怎么算 球体体积面积公式是谁 公式学习




球体表面积公式的推导 圆球表面积公式及证明 球体的表面积怎么算



球面积公式讲解 西瓜视频搜索



圆球表面积 球体表面积的公式证明 篆体字转换器




球的体积公式 球的体积公式画法



基本形狀和3d圖形的數學公式




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org



扇形的体积公式 土嘎嘎



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社



扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili



1



3 9 弧长及扇形的面积 哔哩哔哩 つロ干杯 Bilibili



扇形面积和周长计算公式 关于扇形的所有公式 周长 弧长 半径 圆心角 写得清楚 详细 朵拉利品网



球体体积公式推导图解 万图壁纸网
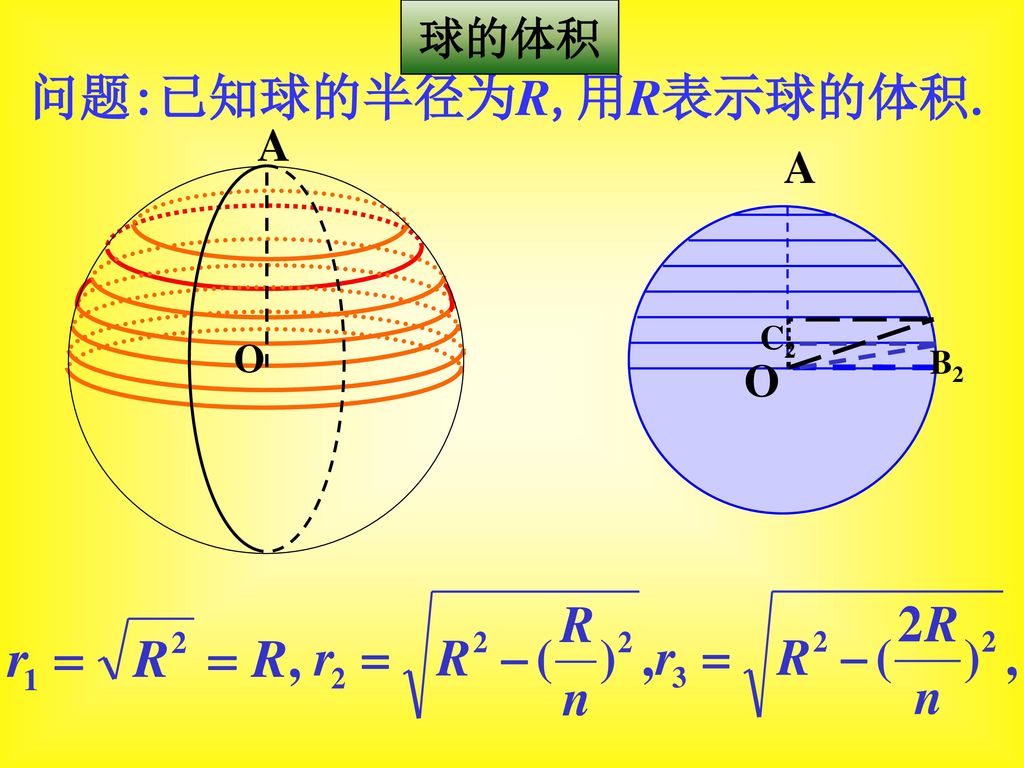



球的体积和表面积ppt Download




球的表面积公式体积公式怎么写来求推导过程 计算机器在线计算



Elyiilt5xxrycm




扇形的面积 弧长 周长 弦长在线计算器 三贝计算网 23bei Com




球表面积计算公式




微积分表面力和运动的球体公式体积基本定理png图片素材免费下载 图片编号 Png素材网



球体面积公式推导图解 搜狗图片搜索




微分でつなげる円や球の公式 すうがくブログ 式変形ch



球体面积公式推导图解 搜狗图片搜索



球体表面积公式 怎样计算球体的表面积



不完整球体表面积求不规则半球体的表面积




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫



球面积公式讲解 西瓜视频搜索



圆锥表面积计算公式圆锥表面积公式大全 异径管表面积计算公式



数学一分钟球的体积公式推导证明 哔哩哔哩 Bilibili



圆台体积公式 万图壁纸网




球体表面积公式 球体体积公式 环球信息网




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



圆台的表面积和体积 文章阅读中心 急不急图文 Jpjww Com




半圆球体积公式



1




球体部分面积计算公式球体表面积公式
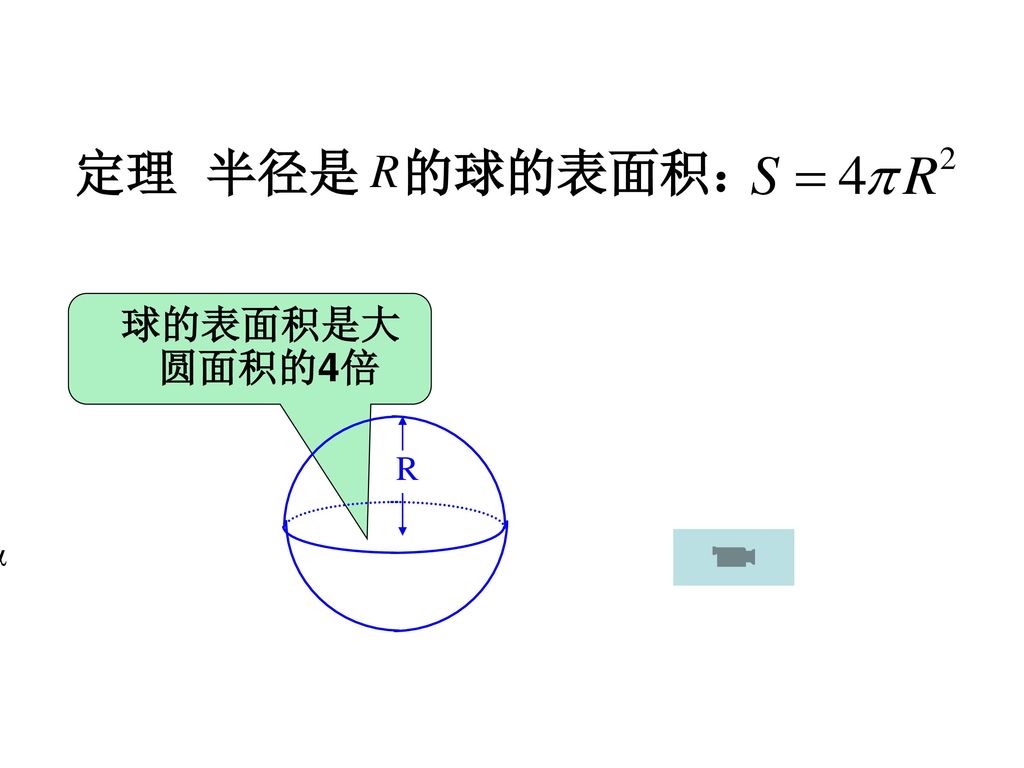



球体表面积



体积公式面积公式 作业 慧海网



球体面积公式推导图解 搜狗图片搜索




圓形周長面積你會背圓的周長和面積公式 但是你知道它們是怎麼來的嗎 Czyk



15複合圓面積數學習作訂正 莊婷纓 楊老師的部落格 痞客邦



在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻



球面积公式讲解 西瓜视频搜索




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网




球的体积公式怎么写 球的体积公式和表面积公式 圆的面积公式



题型 2弧长与扇形面积公式的计算 哔哩哔哩 つロ干杯 Bilibili




球的表面积公式是什么 球体积 表面积公式是




球体表面积计算机



球面积体积公式原理 球形的面积和体积公式 公式学习



写给5年级的学生 球公式是如何推导出来的 表面积



球面积公式讲解 西瓜视频搜索



Python求圆柱体的体积 漫谈超球体的体积公式 斯大林ak47的博客 程序员宅基地 Python求圆柱体的体积 程序员宅基地




求球体的表面积和体积 修也 Csdn博客



球冠 维基百科 自由的百科全书




圆球体总表面积 半径 计算公式 伊迪派



球的表面積的求法 中學數學課 隨意窩xuite日誌



Led屏各种面积 计算办法汇总点击查看 临沂led Led显示屏 临沂全彩显示屏 枣庄led 泰安led 日照led大屏幕 航空箱 航空箱厂家 航空箱生产厂家 山东鹰视电子科技有限公司




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com



扇形面積 面積公式 另解 公式推導過程 中文百科全書




球面積積分球的體積 Itha



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科




球面積公式球 Txfs Co



球的表面积公式推导 万图壁纸网




数学趣谈 球面积公式的不同导出方法 参考网




012 球的体积空间几何体高中数学 Youtube




如何找到球的面积和体积 数学21




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科



圆面积计算公式 生活常识




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com
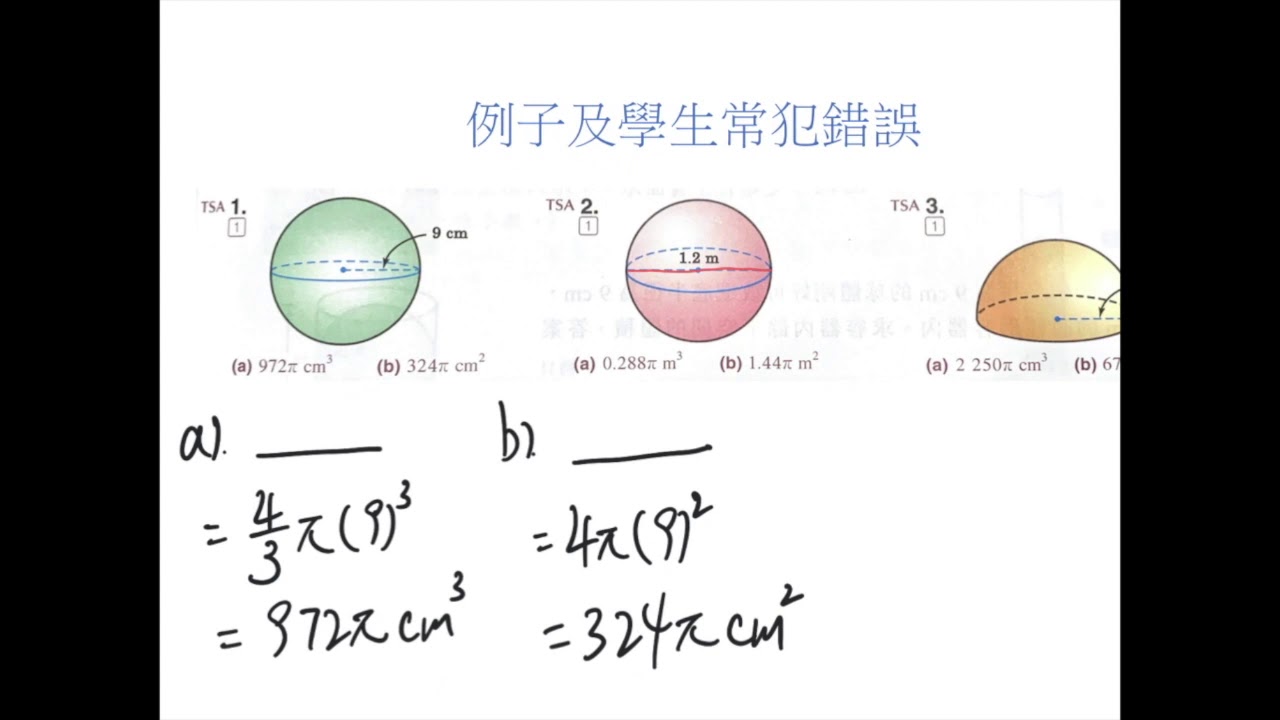



球體體積 總表面面積 Youtube




球の体積と表面積 公式と計算問題と証明 Irohabook



球体表面积公式 100查分网



扇形面积的计算公式 扇形面积的计算公式画法




7 3b球體的表面面積 Youtube




圆的周长和面积公式



0 件のコメント:
コメントを投稿