Standard form to vertex form definitions, facts, and solved examples Cuemath In this minilesson, we will explore the process of converting standard form to vertex form and viceversa The standard form of a parabola is y =ax2 bxc y = a x 2 b x c The vertex form of a parabola is y = a(x −h)2 k y = a ( x − h) 2 kThe Vertex formula of a parabola is used to find the coordinates of the point where the parabola crosses its axis of symmetry The vertex is the point (h,k) As we know the standard equation of a parabola is y = ax 2 bxcVertex Form Of A Quadratic The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertexThe "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or
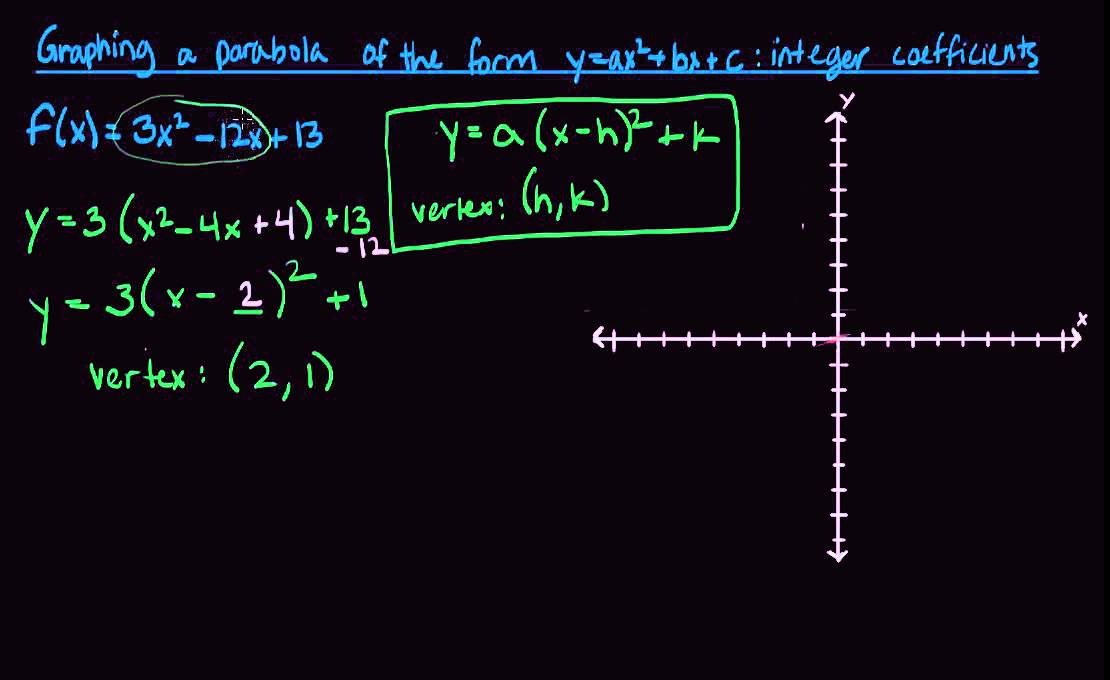
Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
Focus of parabola y=ax^2+bx+c
Focus of parabola y=ax^2+bx+c-To Graph the Quadratic Function \(y = ax^2 bx c\text{}\) Determine whether the parabola opens upward (if \(a \gt 0\)) or downward (if \(a \lt 0\)) Locate the vertex of the parabola The \(x\)coordinate of the vertex is \(x_v =\dfrac{b}{2a}\text{}\) Find the \(y\)coordinate of the vertex by substituting \(x_v\) into the equation of the parabola Explanation Given a parabola equation If the parabola equation is in the form f (x) = Ax2 Bx C = 0 The vertex is ( − B 2A,f ( − B 2A)) Once you have the x value of the vertex, just evaluate the function with that x value Example f (x) = 3x2 −2x −9 x = − −2 2 ⋅ 3 = 2 6 = 1 3 f ( 1 3) = 3(1 3)2 − 2 1 ⋅ 1 3 − 9



Quadratic Function Y Ax2 Bx C When A Is Sutori
I have trouble grasping some basic things about parabolas (This should be easily found on Google, but for some reason I couldn't find an answer that helped me) I know one simple standard equationConvert to vertex form, as necessary Then the the vertex ( h, k) for any given quadratic y = ax 2 bx c obeys the formula Advertisement Practically speaking, you can just memorize that h = – b / (2 a) and then plug your value for " h " back in to " y =" to calculate " k "SOLUTION A parabola y = ax^2 bx c has vertex (4, 2) If (2, 0) is on the parabola, then find the value of abc
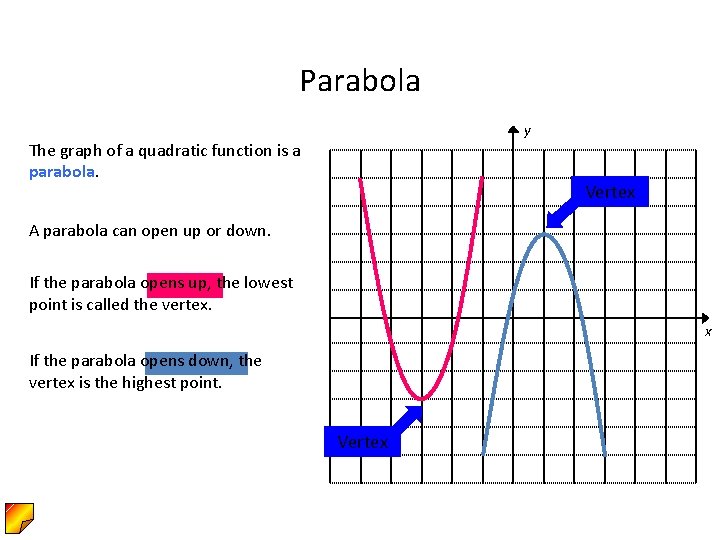
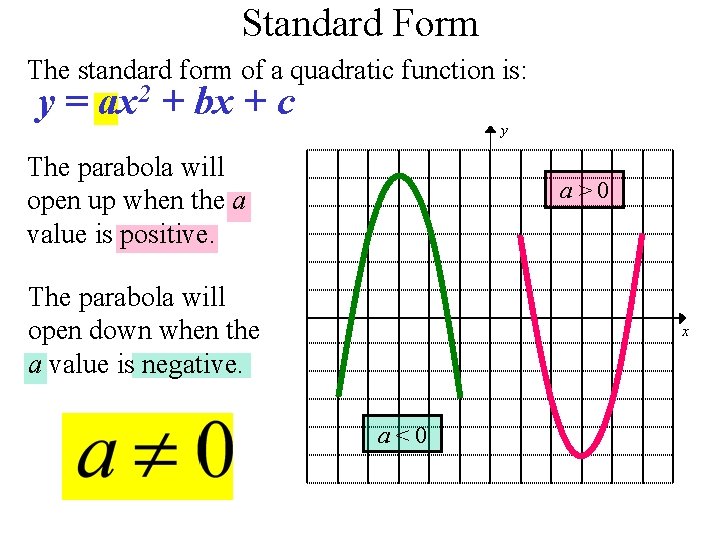
The Graph of y = ax2 bx c 393 Lesson 64 The Graph of y = ax2 bx c Lesson 6–4 2 BIG IDEA The graph of y = ax bx c, a ≠ 0, is a parabola that opens upward if a > 0 and downward if a < 0 Standard Form for the Equation of a Parabola Best Answer Suppose that we have an equation y=ax^2bxc whose graph is a parabola with vertex (3,2), vertical axis of symmetry, and contains the point (1,0)The general form of a quadratic is "y = ax 2 bx c"For graphing, the leading coefficient "a" indicates how "fat" or how "skinny" the parabola will beFor a > 1 (such as a = 3 or a = –4), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample values
Of that vague equation, the X coordinate is at b/2a To find the Y coordinate, plug it back in Now if you would like to do this the calculus way, differentiate the equation, and set the resulting 2ax = b and solve for X Then, plug the X backThe graph of a quadratic function y = ax^2 bx c is shown Tell whether the discriminant of ax^2 Find the equation of the parabola y = ax^2 bx c that is tangent to the line y = x 1 at (0,1) Find the ycoordinate of the vertex of the parabola whose equation is y=x^2x2 Find the ycoordinate of the vertex of the parabola whoseA there are 2 x intercepts, the vertex below the xaxis, and a >0 b there is 1 xint and the vertex is o the x axis c there are 2 x int the vertex below is the x axis and a 0




Quadratic Function
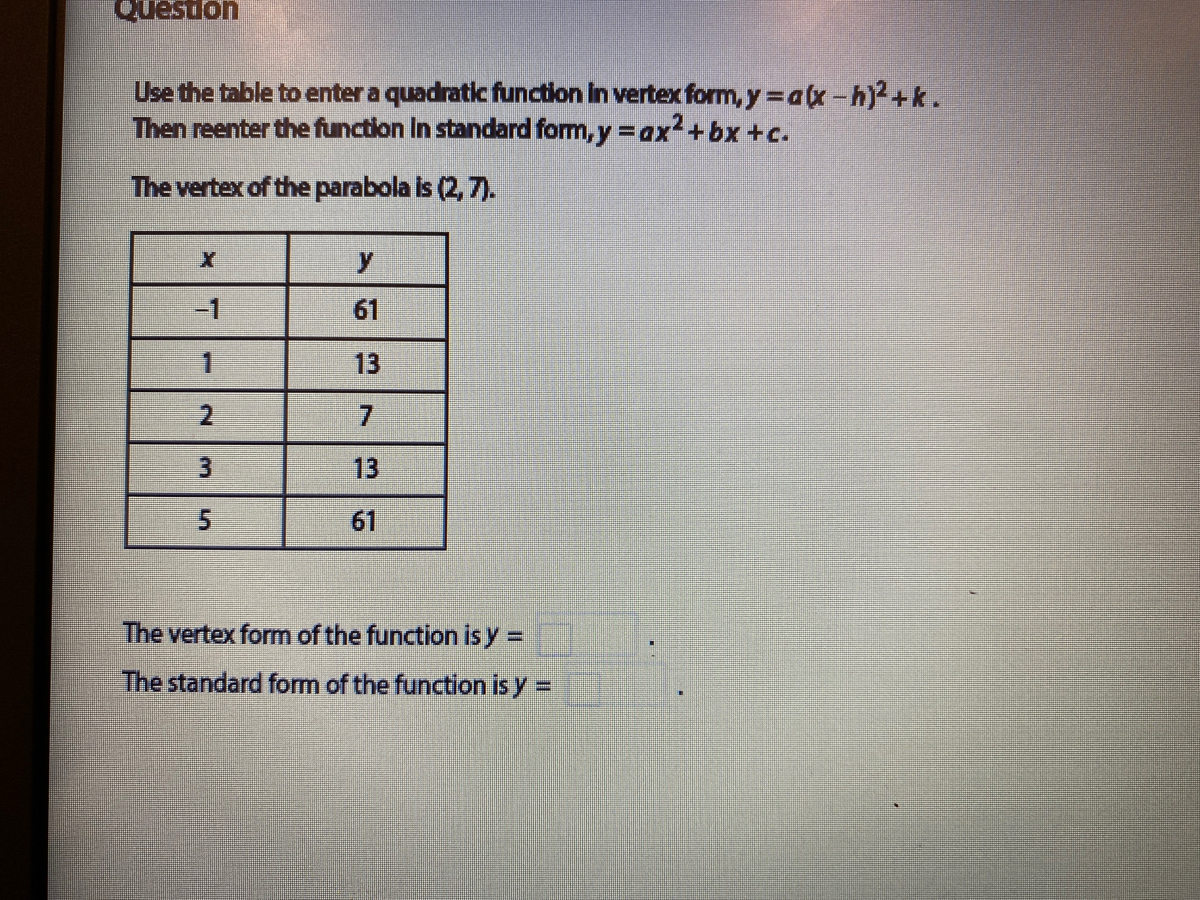



Answered Use The Table To Enter A Quadratic Bartleby
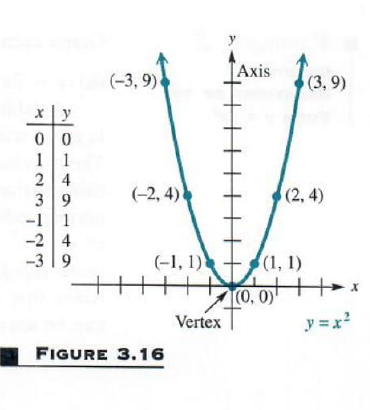
In the figure, the vertex of the graph of y=x 2 is (0,0) and the line of symmetry is x = 0 Definition Parabola 1Algebric A Parabola is the graph of a quadratic relation of either form where a ≠ 0;If a < 0 , the parabola has its concavity turned down;Click here👆to get an answer to your question ️ Suppose a parabola y = ax^2 bx c has two x intercepts one positive and one negative, and its vertex



Standard Form



Lessons 5
👉 Learn how to graph quadratic equations in vertex form A quadratic equation is an equation of the form y = ax^2 bx c, where a, b and c are constants The Standard form of a Parabola is y = a x 2 b x c y=ax^2bxc y = ax2 bx c To obtain the Standard Form from the Vertex Form we use these steps y = a ( x − h) 2 k y=a (xh)^2k y = a(x − h)2 k y = a ( x 2 − 2 h x h 2) k y=a (x^22hxh^2)k yGraphing Parabolas Not in Vertex Form Here are the steps required for Graphing Parabolas in the Form y = ax 2 bx c Step 1 Find the vertex There are two ways to find the vertex, the first way to find the vertex is to complete the square which will lead to the equation y = a (x – h) 2 k, in which case this vertex is at the point (h, k)



Quadratic Functions




Quadratic Function
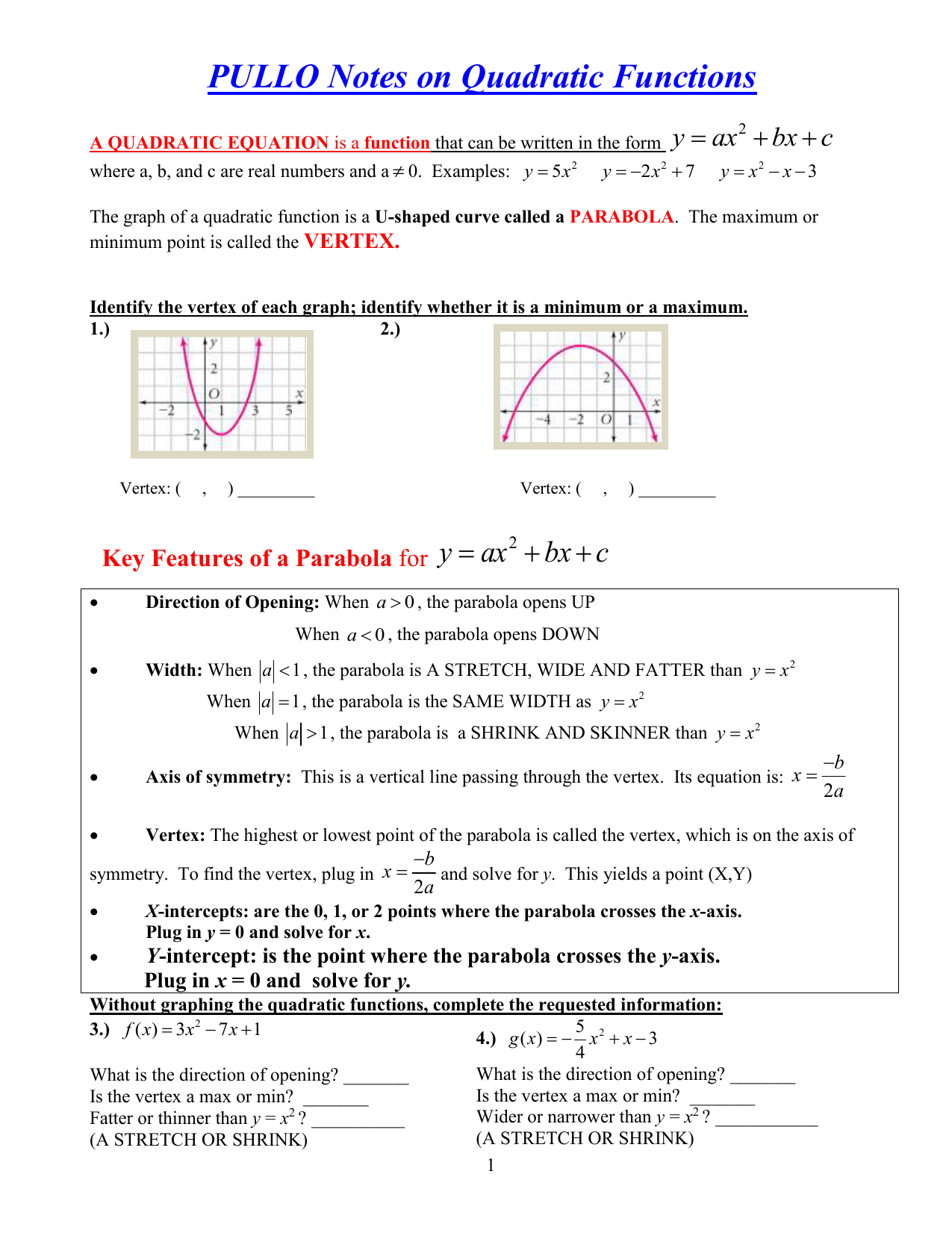
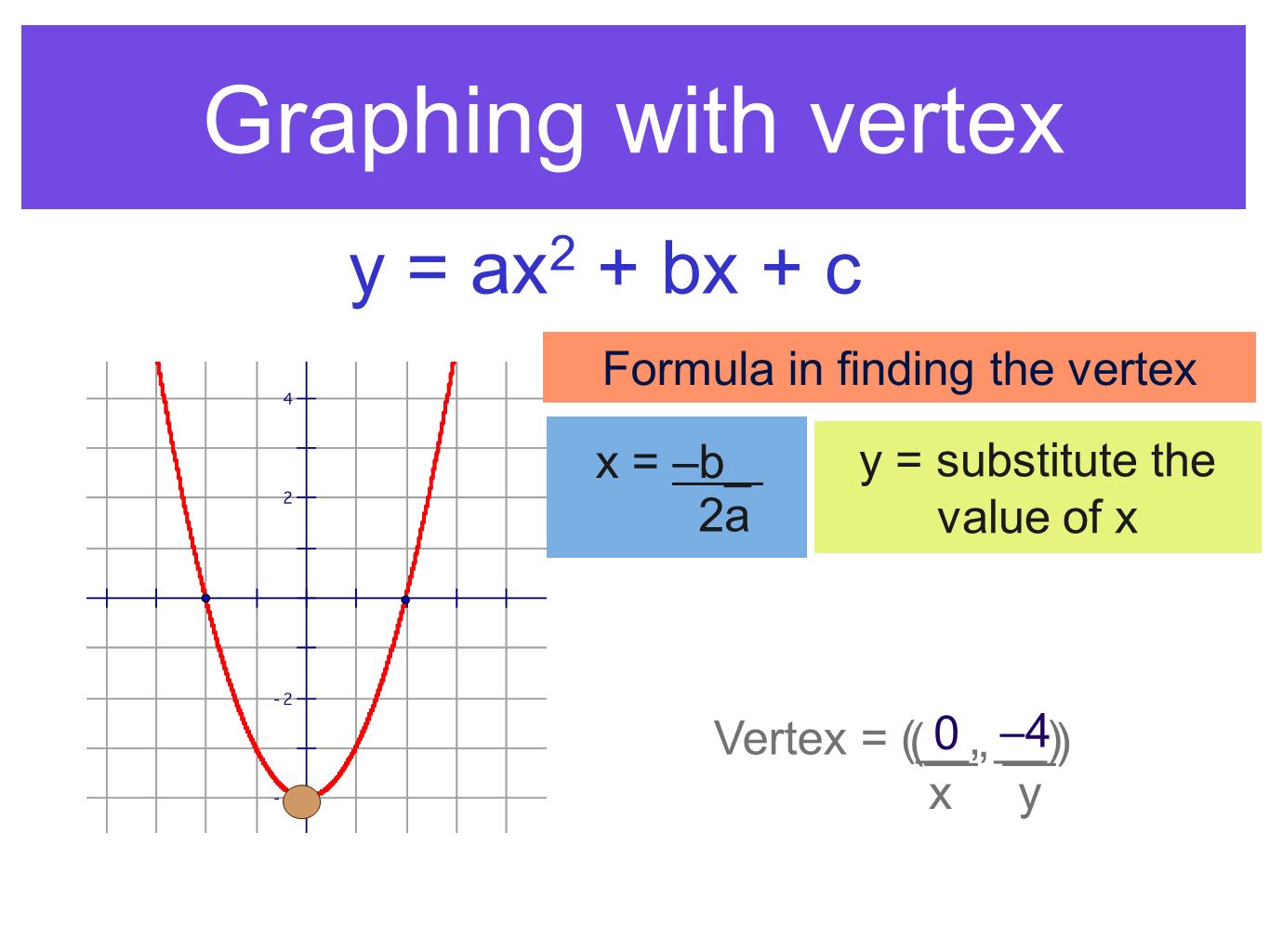
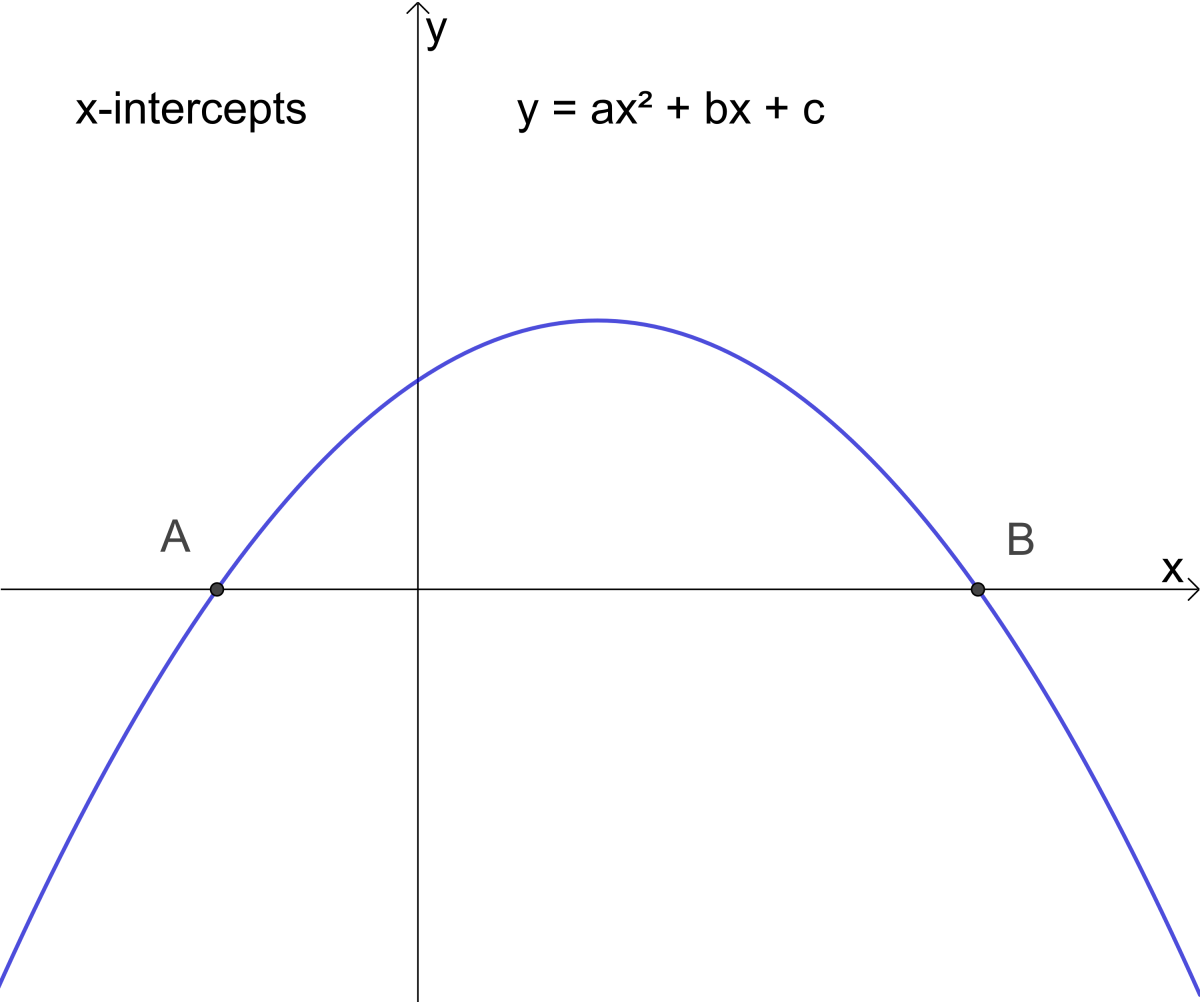
Step 1 Solve for the vertex of the parabola The vertex of a parabola of the form {eq}y= x^2 bx c {/eq} is always given by {eq}\left (\dfrac {b} {2a},f (\dfrac {b} {2a})\right) {/eq} StepAnswer y = ax2 bxc The vertex will correspond to the point where the curve attains a minima (a> 0) or maxima (a < 0) ∴ dxdy = 2axb = 0 ⇒ x = 2a−bGiven a parabola y = a x 2 b x c, the point at which it cuts the y axis is known as the y intercept The y intercept will always have coordinates (0, c) where c is the only term in the parabola 's equation without an x



Lessons 5
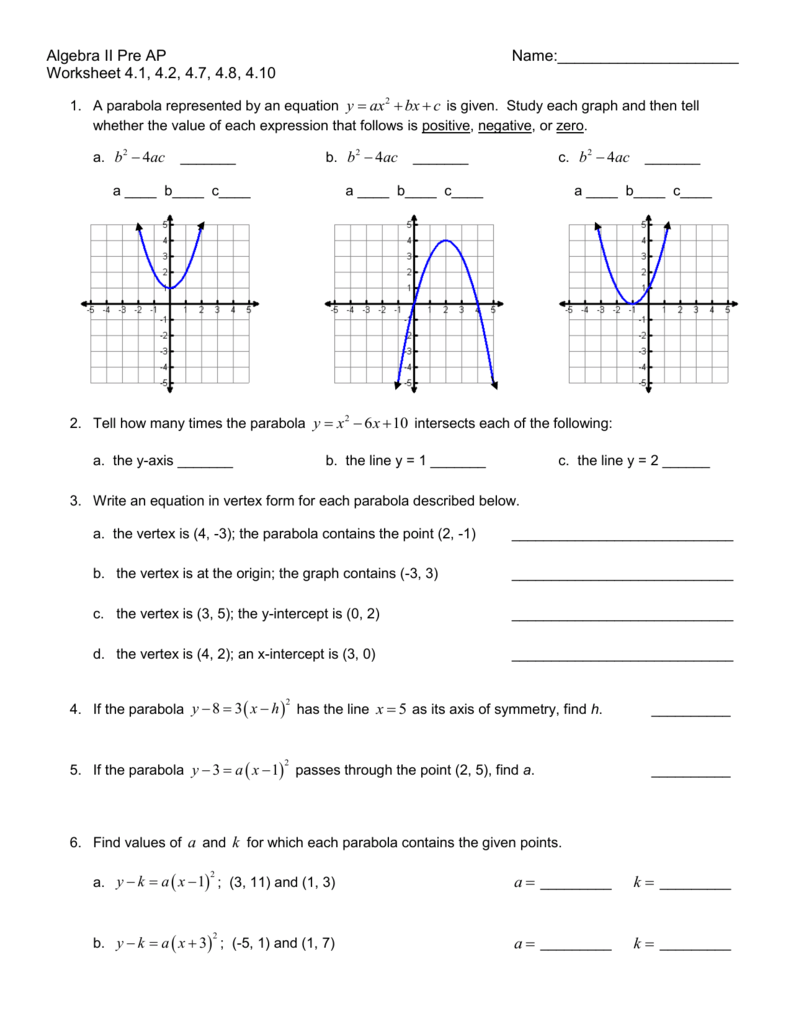



H Gt Algebra 2 Worksheet 4
Transform the general equation y=ax^2bxc to vertex form, where the vertex= (h,k)Exploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the thirdParabolas The graph of a quadratic equation in two variables (y = ax2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola



Solution A Parabola Y Ax 2 Bx C Has Vertex 4 2 If 2 0 Is On The Parabola Then Find The Value Of Abc
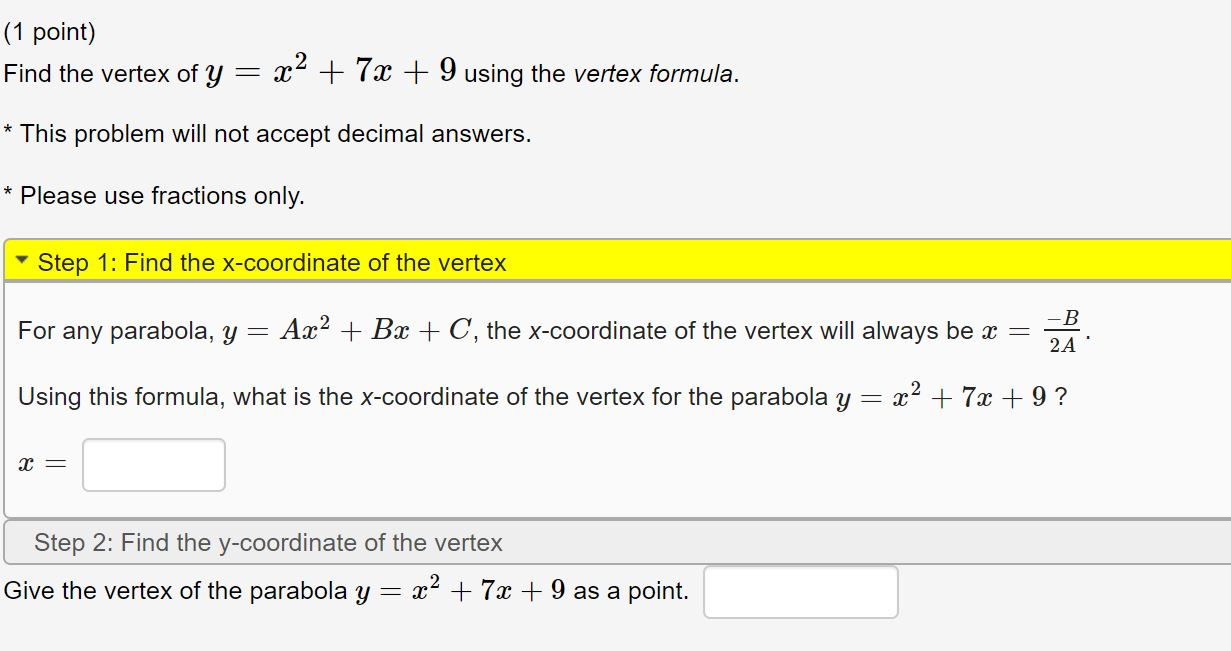



Solved 1 Point Find The Vertex Of Y 63 2 Using The Vert Chegg Com
Which description of the graph of y= ax^2 bx c is not possible?Solutions for Chapter 31 Problem 63E Derive the formula for the xcoordinate of the vertex of parabola y = ax2 bx c Hint The slope is zero at the vertex, so finding the vertex means finding the critical number Get solutions Get solutions GetIt is the lowest or highest point on the parabola, depending on whether the parabola opens upwards or downwards



Quadratic Graph Example Y Ax Expii




1 The Standard Form Of A Quadratic Equation Is Y Ax 2 Bx C 2 The Graph Of A Quadratic Equation Is A Parabola 3 When A Is Positive The Graph Opens Ppt Download
Learn termquadratics = y = ax^2 bx c with free interactive flashcards Choose from 68 different sets of termquadratics = y = ax^2 bx c flashcards on Quizlet To find corresponding value of ycoord of vertex , substitute x = 2 into the function x = 2 y = −(2)2 4(2) −3 = − 4 8 − 3 = 1 ⇒ vertex = ∣∣ ∣ ∣¯¯¯¯¯¯¯¯¯¯¯¯¯¯a a 2,1 a a ∣∣ −−−−−−− − Here is the graph of y#= x^24x3 graph {x^24x3 10, 10, 5, 5} Answer linkFind in the form y= ax^2 bx c, the equation of the quadratic whose graph a) touches the xaxis at 4 and passes through (2,12) b) has vertex (4,1) and passes through (1,11) Answer provided by




A Parabola Y A X 2 B X C Has Vertex 4 2 2 0 Is On The Parabola Then Abcepuals
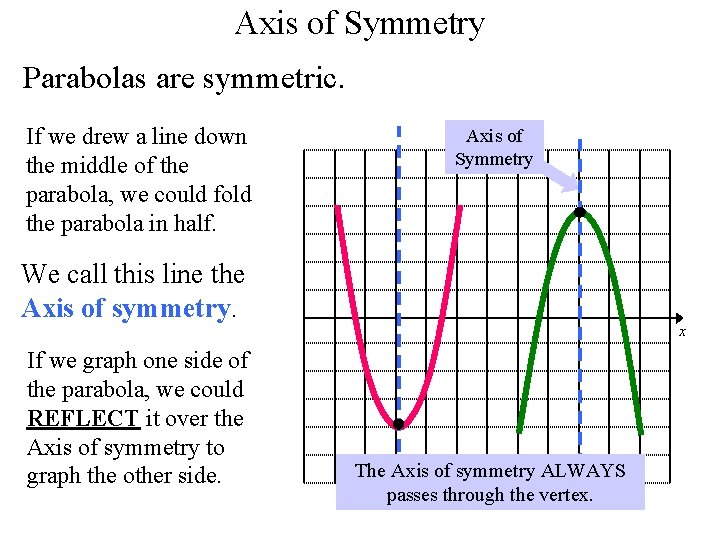



Quadratic Function Y Ax 2 Bx C Quadratic
MathsGee Answers is a global, STEMfocused Q&A platform where you can ask people from all over the world educational questions for improved outcomes The given parabola y = ax2 bx c y = a x 2 b x c doesn't intersect the Xaxis and passes from the points A(−2, 1) A ( − 2, 1) and B(2, 9) B ( 2, 9) Find all the possible values of theThe form y = ax 2 bx c provides the yintercept of the graph, the point (0, c), and the quadratic formula is based in the values of a, b, and c to find the zeros of the graph Example The graph of y = 2x 2 4x 6 has yintercept (0, 6) and using the quadratic formula its zeros are The vertex form of a quadratic is given by y = a(x – h) 2 k, where (h, k) is the vertex The "a" in the vertex form is the same "a" as in y = ax 2 bx c (that is, both a's have exactly the same value) The sign on "a" tells you whether the quadratic opens up or opens down



Graphing Quadratic Functions



1
Find abc if the graph of the equation y=ax^2bxc is a parabola with vertex (5,3), vertical axis of symmetry, and contains the point 0 a parabola y=ax2bxc with axis of symmetry x=c intersects a straight line y=axb at two points, the vertex of the parabola V(c,d) and anothe point WFind a set of numbers a,b,c (not 0) that satisfy this situationShow that there are more than one set of numbers that satisfy this situation and estmate how many there are Submitted8 years agoX = 0 = Y ==> x = b/2a and y = c a (b/2a)²
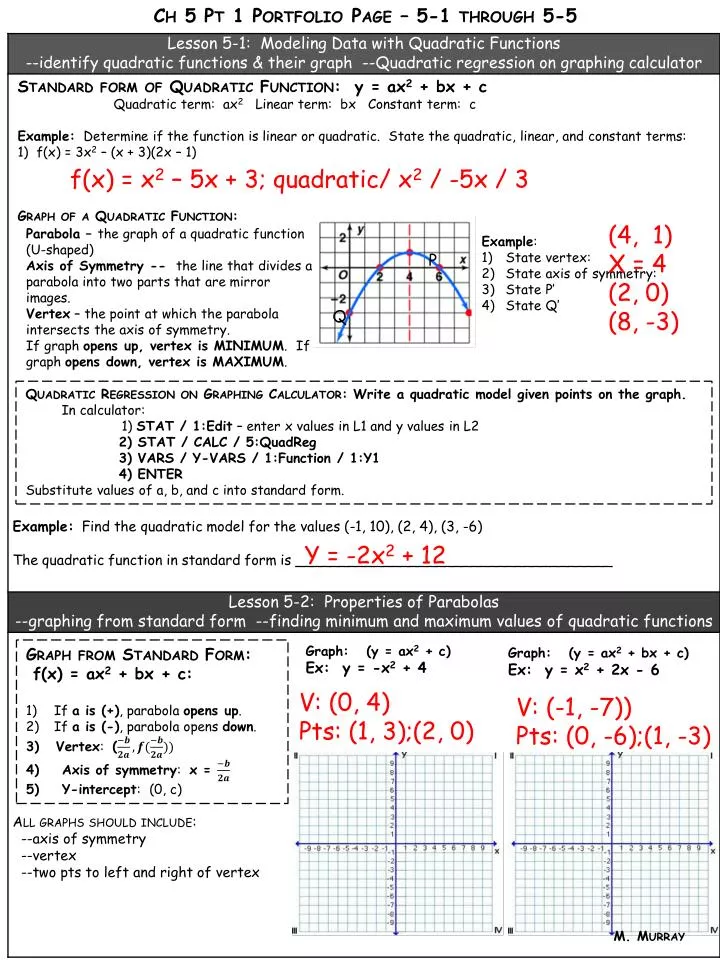



Ppt Standard Form Of Quadratic Function Y Ax 2 Bx C Powerpoint Presentation Id



Http Www Intellichoice Org Wp Content Uploads 16 08 18 Quadratic Functions And Graphs Pdf
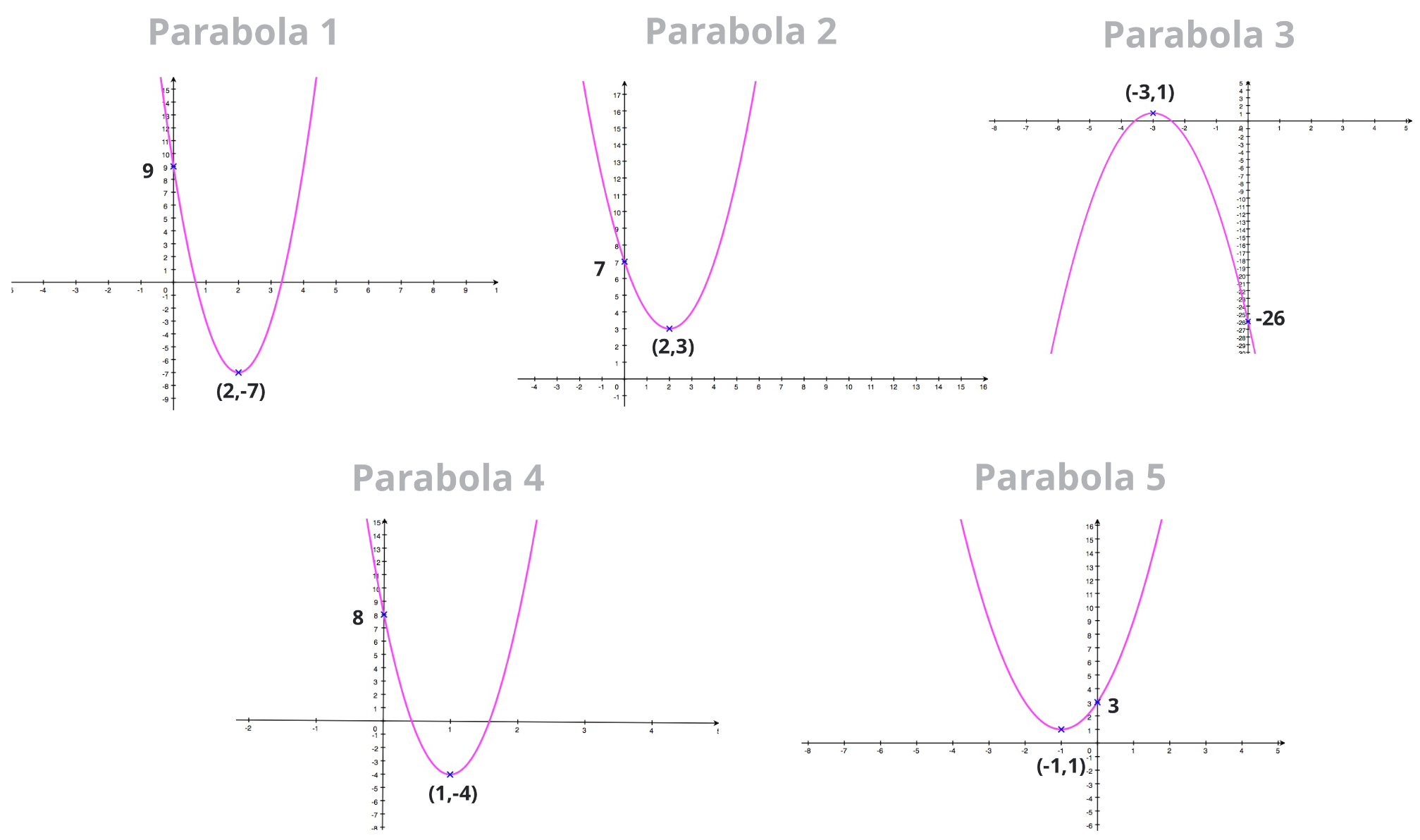
The vertex of $y=ax^2bxc$ Set $a=1$, $b=4$, and $c=2$ to look at the graph of $y=x^24x2$ Using the formula $$x=b/{2a}$$, you can calculate that the axis of symmetry of this parabola is the line $x=2$ Also, notice that the vertex of this parabola is the point $(2,2)$ Now slide $c$ to 45 Consider the parabola $\rho$ given be the equation $y = ax^2 bx c$ Recall that varying $a$ in this equation stretches/squashes $\rho$ and that varying $c$ shifts $\rho$ vertically The change in the parabola $\rho$ as you vary the value of $b$ is a bit harder to describe, but as you vary $b$ , the vertex of $\rho$ traces out a familiar curve A quadratic equation in two variables, where a, b, and c are real numbers and \(a \ge 0\) is an equation of the form \(y=ax^2bxc\) vertex The point on the parabola that is on the axis of symmetry is called the vertex of the parabola;



Sat Math Grid Ins Question 97 Answer And Explanation Cracksat Net



Standard Form Of A Quadratic Function
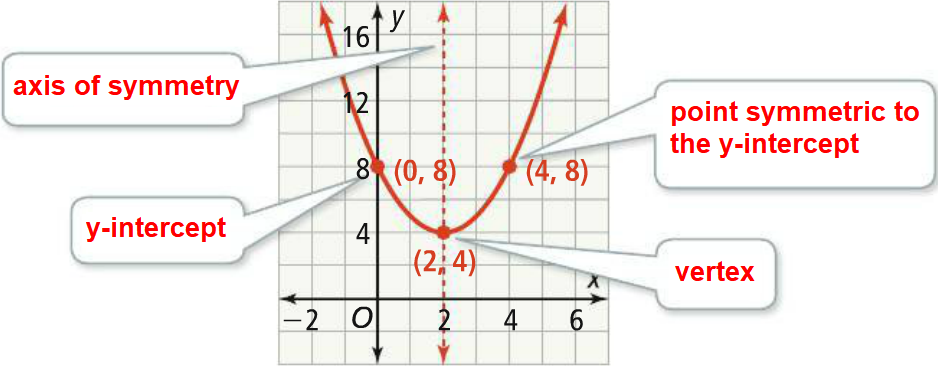
Identifying the Vertex as Max or Min Given the Graph Identifying the Vertex as Max or Min Given Standard Form Finding the Vertex Given Standard Form Finding the Axis of Symmetry Graphing y = ax 2 bx c Using the Table of Values Graphing y = ax 2 bx c Using the Vertex Word Problems Involving Graphing Quadratic FunctionsThe coefficient c controls the height of the parabola;The parabola has so far been defined as the graph of the function y = ax 2 bx c There is also a geometric definition of the parabola in terms of the path traced out by a moving point (Such a graph is known as a locus )



Vertex Form How To Find The Equation Of A Parabola



How To Show That The Vertex Of The Parabola Math Y Ax 2 Bx C Math Can Be Expressed As Math B 2a C B 2 4a Math Quora
The graph of the function in the previous example is f (x) = x 2 – 5x 6 Plotting the graph of a quadratic function y = ax 2 bx c, one will notice that if a > 0 , the parabola has its concavity turned up;Graphing Quadratic Functions of the Form y = ax 2 bx c — Graphing y = ax 2 bx c Using the Vertex and Axis of Symmetry Explore More at 0/0 The standard form of a parabola equation is y=ax^ 2 bxc Input the values of a, b and c, our task is to find the coordinates of the vertex, focus and the equation of the directrix The vertex of a parabola is the coordinate from which it takes the sharpest turn whereas y=a is the straightline used to generate the curve



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau



Which Is The Coordinate Of The Vertex Of Y Ax 2 Bx C Quora
To find the vertex of a quadratic equation, y = ax 2 bx c, we find the point (b / 2a, a(b / 2a) 2 b(b / 2a) c), by following these steps Get the equation in the form y = ax 2 bx c How to Find the Vertex of a Quadratic Equation Video Vertex is the leading and mosttrusted provider of comprehensive, integrated taxHence, it is also called the turning point If the quadratic function is in vertex form, the vertex is (h, k) Using the method of completing theY = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, y



If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community



Vertex And Intercepts
Y = ax 2 bx c or x = ay 2 by c 2 Geometric A parabola is the set of all points in aAn incomplete quadratic equation is of the form ax 2 bx c = 0, and either b = 0 or c = 0 Solve quadratic equation with StepbyStep Math Problem Solver The graph of a quadratic equation (y = ax 2 bx c) is the shape of a parabola A parabola looks like a U or an upsidedown U The vertex of a quadratic equation is the maximum or minimumMore specifically, it is the height of the parabola where it intercepts the yaxis Vertex The vertex of a parabola is the place where it turns;




Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube



Graphing Quadratic Equations Functions Parabolas By Finding Vertex Worksheet
Standard Form The standard equation of Parabola is y=ax2bxc Vertex Form The Vertex form of the quadratic equation of Parabola is y = (x – h)2 k, here (h,k) are the points on the xaxis and yaxis respectively As we have seen Parabola has two different forms of equations The method to find Vertex is different for both forms ofThe given equation y = ax^2 bx c may be written as (y c) = )x) = ) (y c a (b/2a)²) or X² = 4bY where X = (x b/2a) and Y = (y a (b/2a)² c) and 4b = 1/a Therefore, vertex V of this parabola is given by; Show that y = ax 2 bx c, a ≠ 0 represents a parabola and find its vertex, focus, directrix and latus rectum



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




How Does The Vertex Location Of A Parabola Change Wolfram Demonstrations Project



Solve Quadratic Relation Parabolas Step By Step Math Problem Solver




Standard Form To Vertex Form Without Completing The Square Method Algebra 2 Youtube



What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora
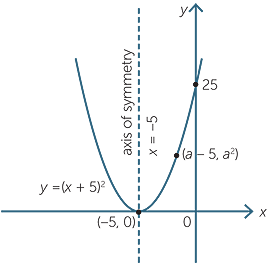



Quadratic Function



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id




Finding The Vertex Of A Parabola In Standard Form Video Khan Academy
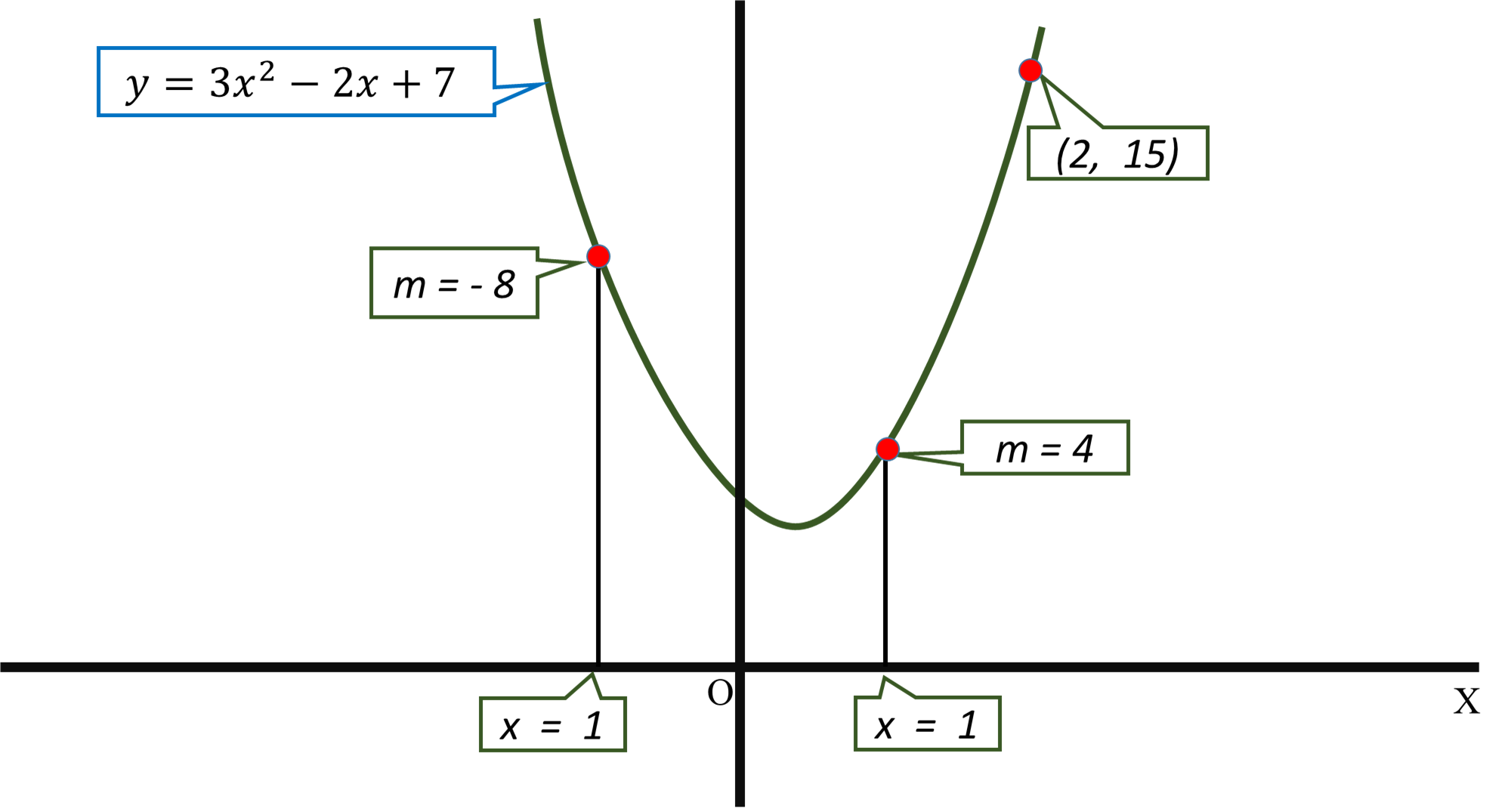



How Do You Find A Parabola With Equation Y Ax 2 Bx C That Has Slope 4 At X 1 Slope 8 At X 1 And Passes Through 2 15 Socratic
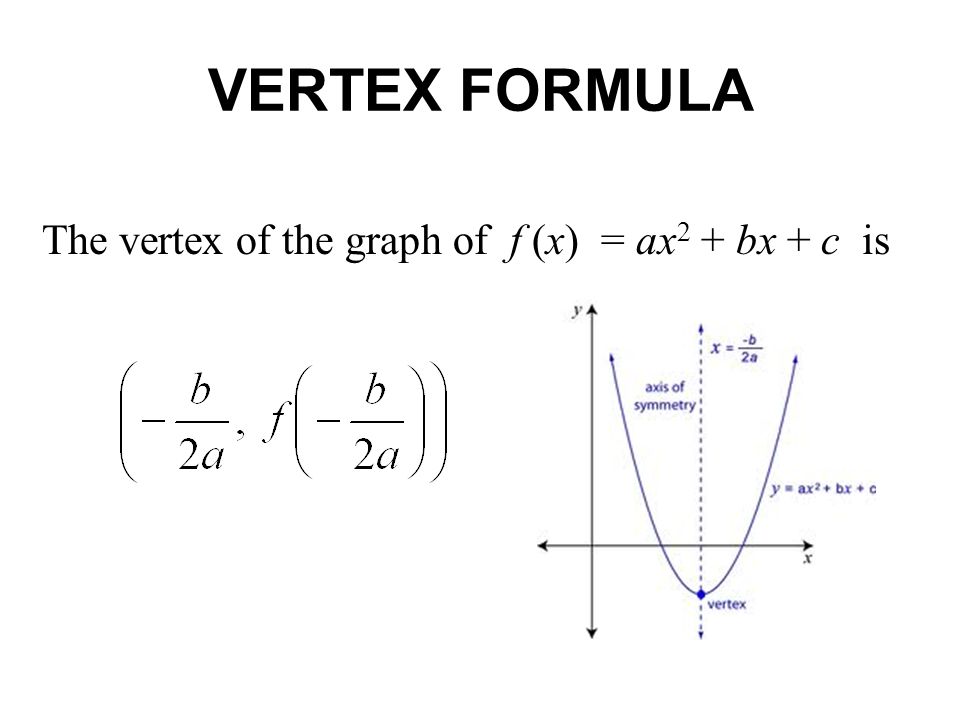



Quadratic Functions And Modeling Ppt Video Online Download



Quadratic Functions Notes Pullo 3



Parabola Conic Section Ppt Download



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego




2 4 Grapgs Of Second Degree Functions



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola



Finding A Quadratic Function With A Parabola Studypug



How To Show That The Vertex Of The Parabola Math Y Ax 2 Bx C Math Can Be Expressed As Math B 2a C B 2 4a Math Quora




Prove That The Graph Of The Parabola Y Ax 2 Bx Chegg Com




Find The Sign Of A B C In Ax 2 Bx C Given The Graph And A Coordinate On It Mathematics Stack Exchange



Graphing Quadratic Functions The Leading Coefficient The Vertex
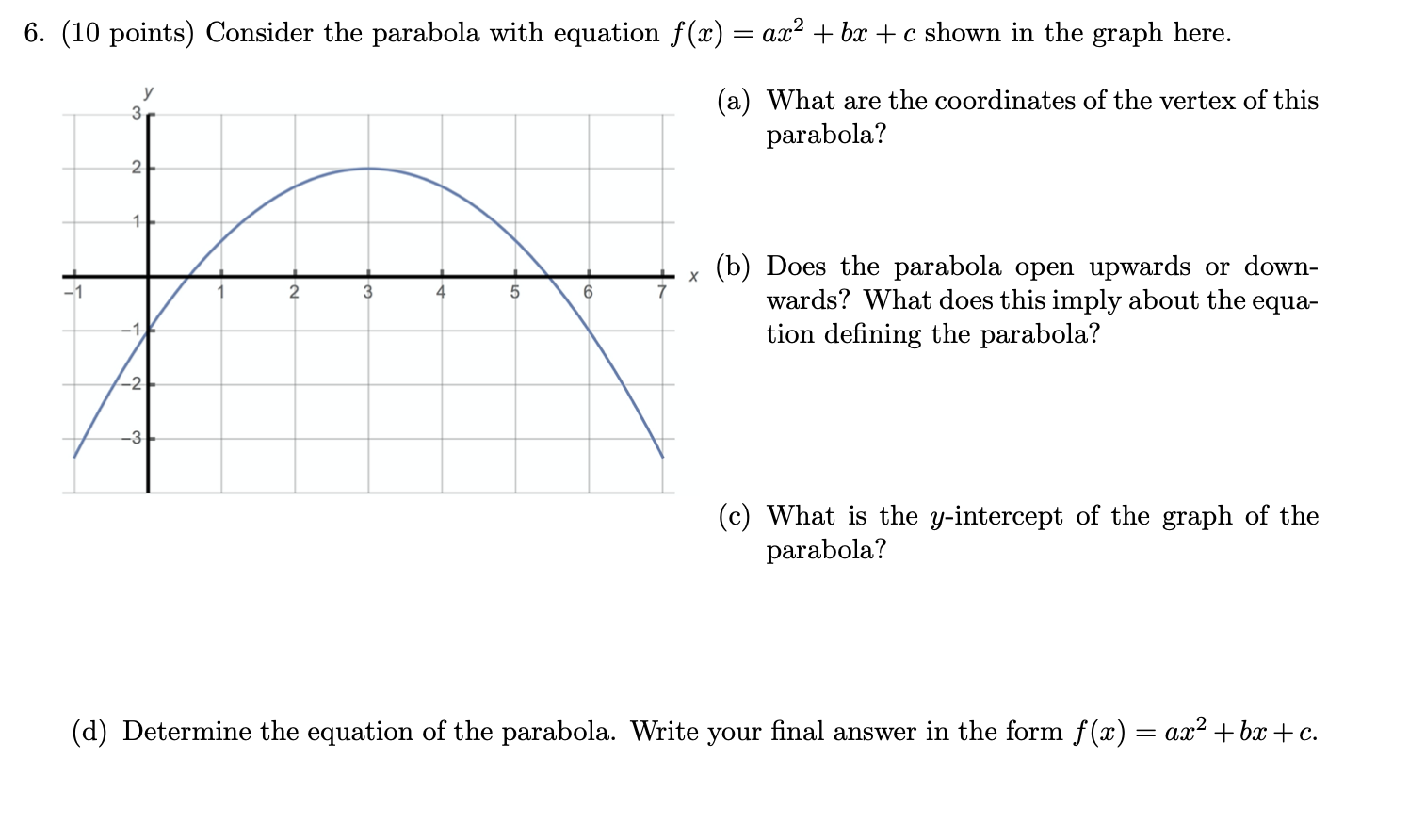



6 10 Points Consider The Parabola With Equation Chegg Com




2 4 Grapgs Of Second Degree Functions




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download



Parabola



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math




Quadratic Function Y Ax2 Bx C When A Is Sutori



Quadratic Graph Example Y Ax Expii
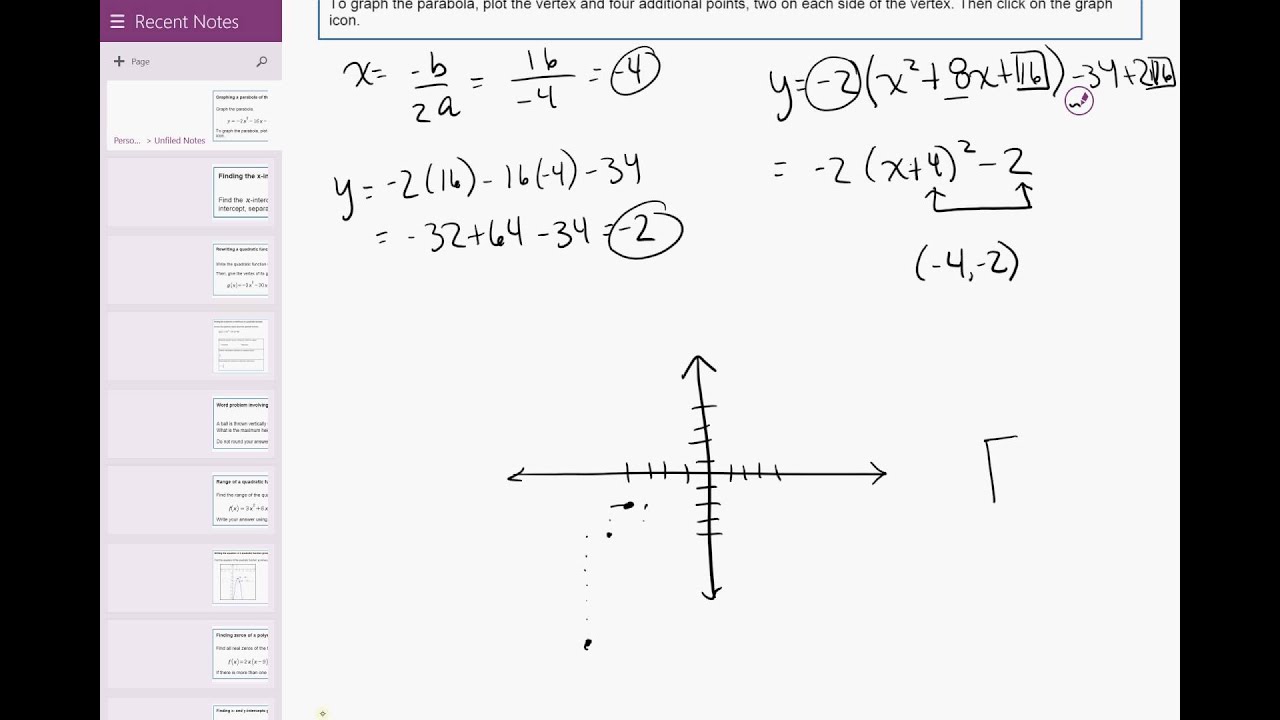



15 04 Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Positive And One Negative And Its Vertex Is 2 2 Sarthaks Econnect Largest Online Education Community




Graphing Parabolas




How To Find The Vertex Of A Quadratic Equation Video Lesson Transcript Study Com




Graph Of Y Ax 2 Bx C Novocom Top



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
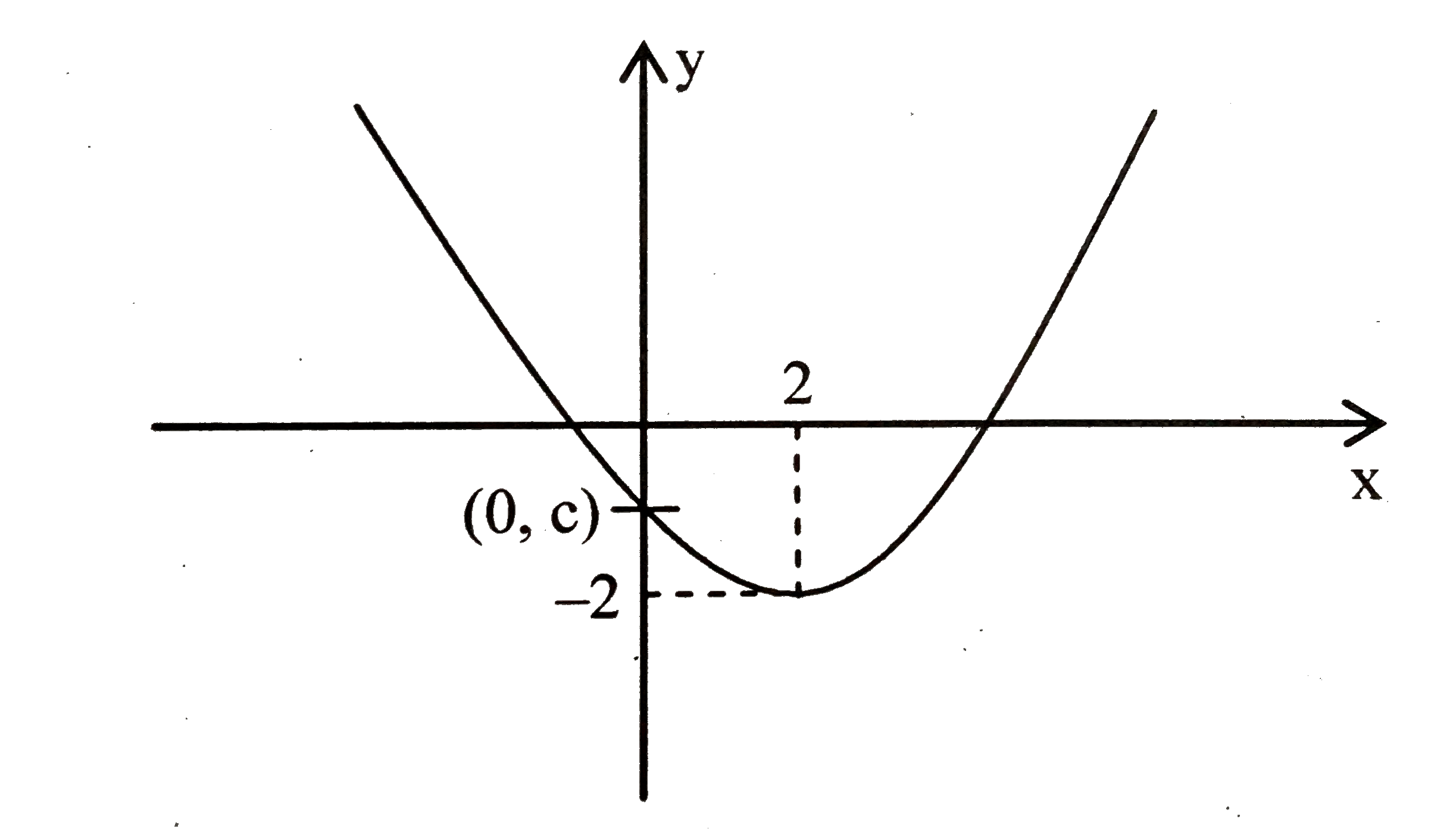



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos
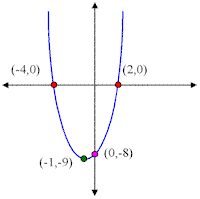



Parabolas
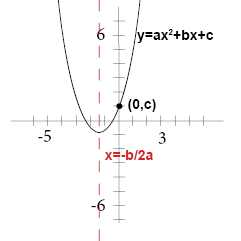



How Do You Graph F X 3x 2 4x 1 Socratic
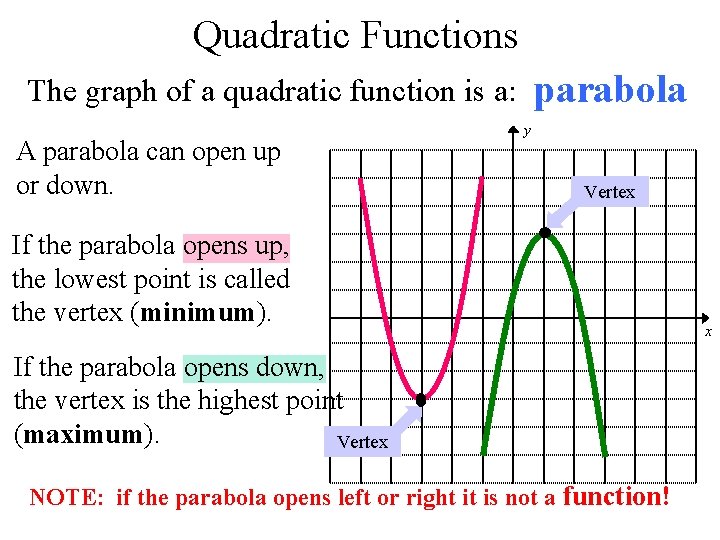



Quadratic Function Y Ax 2 Bx C Quadratic




A Parabola Y A X 2 B X C Has Vertex 4 2 2 0 Is On The Parabola Then Abcepuals
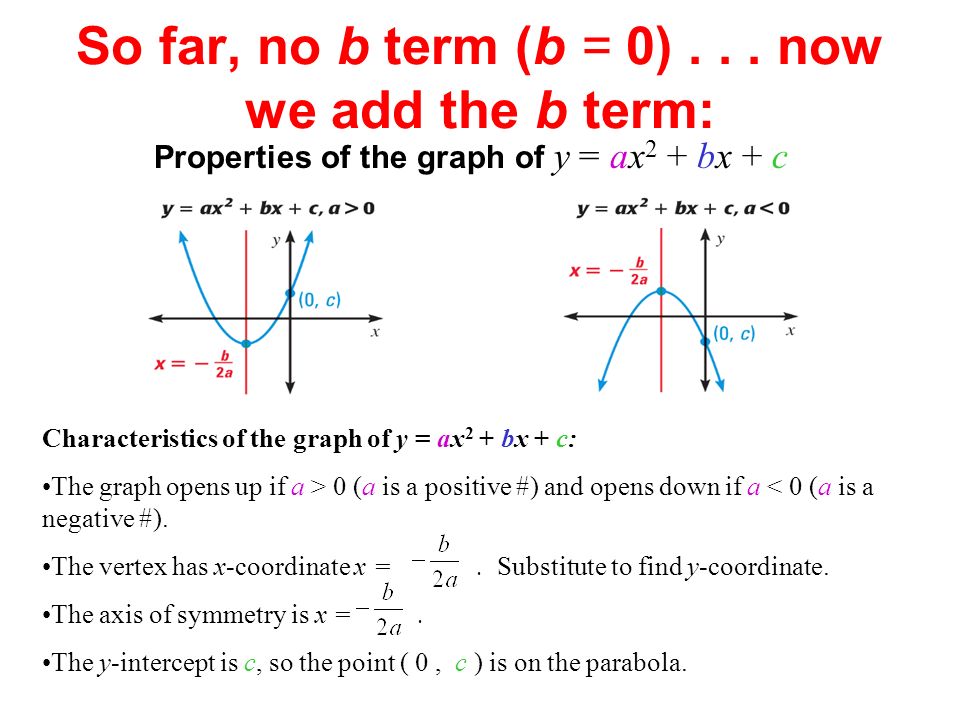



Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Axis Of Symmetry Of A Parabola



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego




The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com



Vertex Directrix And Focus Of Quadratic Equations
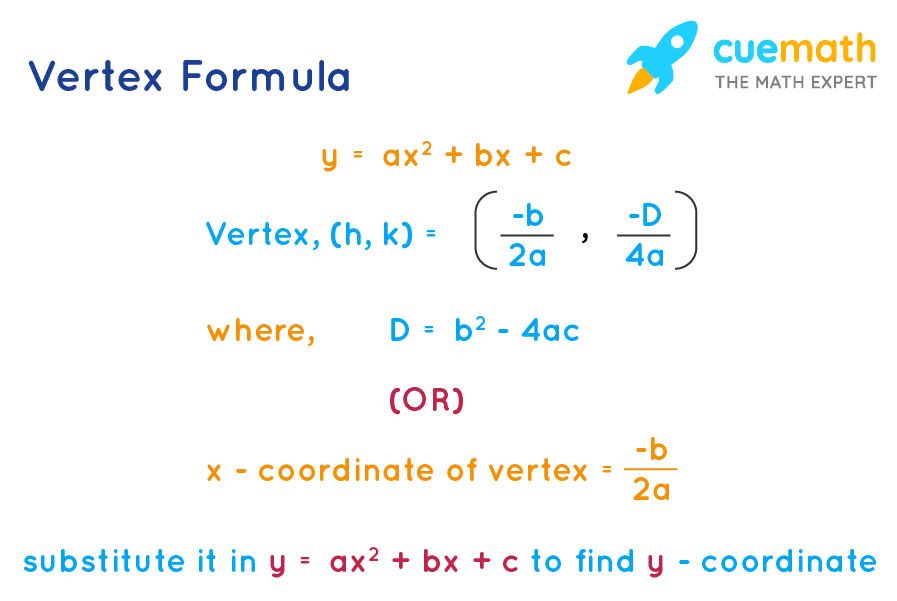



Vertex Formula What Is Vertex Formula Examples




Quadratic Function Wikipedia




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



Transformations Of Equations Of Parabola Parametric Equations Of Parabola



Assignment 2



1
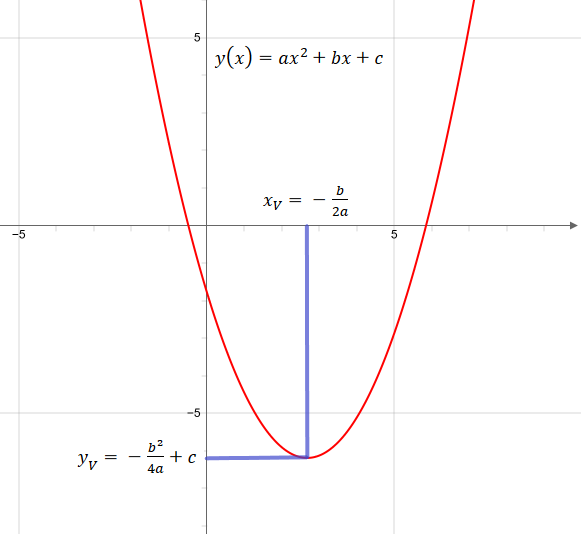



Online Calculator For Converting Quadratic Equation From Normal Form To Vertex Form
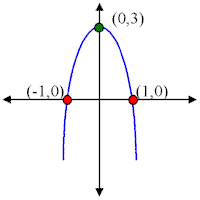



Parabolas



Unique Quadratic Equation In The Form Y Ax 2 Bx C



When Looking At A Parabola In The Form Ax 2 Bx C I Know The Vertex Is Given By B 2a And F B 2a But Why Is This The Case Quora




Focus Of Parabola Y Ax 2 Bx C Is



Unique Quadratic Equation In The Form Y Ax 2 Bx C



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora



Graphing Quadratic Functions Y 2 Ax Bx C



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Graphing Y Ax2 Bx C Youtube




This Is What The Problem Says Assuming All Parabolas Are Of The Form Y Ax 2 Bx C Drag And Drop The Brainly Com




Finding The Parts Of A Parabola Ck 12 Foundation



Quadratic Function Y Ax 2 Bx C Quadratic




B Value Definition Explanation Video Lesson Transcript Study Com




Quadratic Function Wikipedia



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation
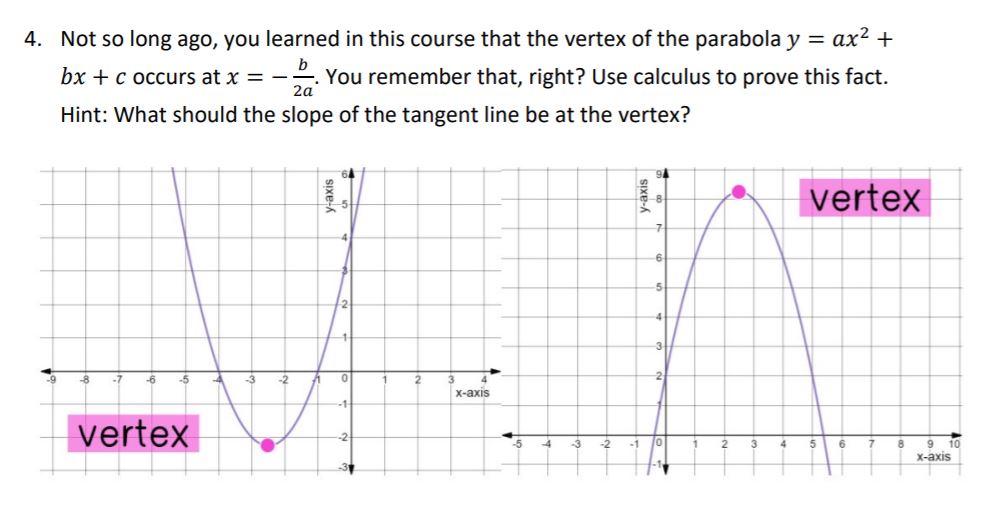



Answered Not So Long Ago You Learned In This Bartleby




Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos




Quadratic Function




The Given Figure Shows The Graph Of The Polynomial F X Ax 2 Bx C Then Ltbr Gt 1 Nbsp Youtube




Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download



View Question Find A B C If The Graph Of The Equation Y Ax 2 Bx C Is A Parabola With Vertex 5 3 Vertical Axis Of Symmetry And Contains The



Quadratic Graph Example Y Ax Expii



Show That Y Ax 2 Bx C A 0 Represents A Parabola And Find Its Vertex Focus Directrix And Latus Rectum Sarthaks Econnect Largest Online Education Community



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego



0 件のコメント:
コメントを投稿