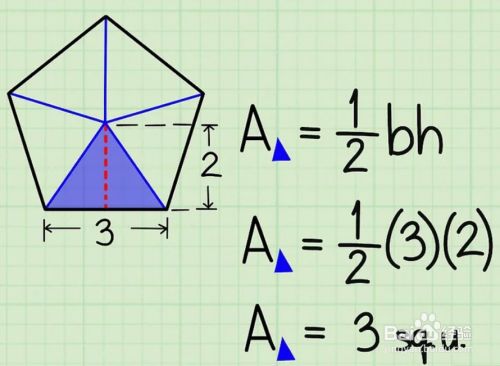
· 正多角形の問題では、正三角形、正方形、正六角形、正八角形、正五角形の順によく出題されます。ちなみに、正多面体では、正四面体ですね。 スポンサーリンク 正三角形の面積 正三角形の面積を求めて、それを利用した問題はよく出題されます。その例が正六角形の体積などもその1つでここでは、半径1の円に内接する正五角形の一辺の長さを計算して、正五角形の作図方法を説明します。 正五角形の内角は 2π/5 2 π / 5 ラジアン(72°)であることから、 まず最初に a=cos(2π/5) a = cos ( 2 π / 5) を使って一辺の長さを計算します。 右の図に1 辺の長さが分かっている時は公式を用いる 基本の六角形は6つの二等辺三角形で構成されているので、その公式もまた二等辺三角形の面積を求める公式が元になっています。 六角形の面積(A)を求める公式は A = (3√3 s2)/ 2 となり、 s が辺の長さを指しています。 {"smallUrl""https\/\/wwwwikihowcom\/images_en\/thumb\/e\/eb\/CalculatetheAreaofa
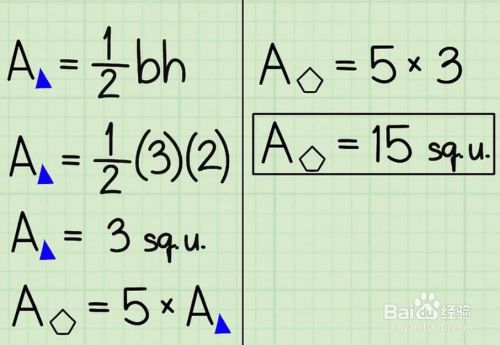
正五边形面积怎么求 百度经验
正五角形 面積 公式
正五角形 面積 公式-五芒星(星型正五角形)の形 星型正多角形のデザインで有名なものに、魔術的なデザインとして知られる「五芒星」があります。 この星型五角形(五芒星)を含めた星型正n角形について、今回、まったく新しい視点で、面積の一般公式を導き出しました。 実は、手の爪に塗られた星のマニキュアを見て、爪の中に一体、どのぐらい大きな星型が描けるだろうかと · 三角形の面積が 底辺×高さ÷2であることが理解できていると仮定します。 式から 底辺が同じ長さで高さが同じなら面積は同じであることがわかります。 正多角形を適当にいくつかの三角形に分けます。 例えば、正五角形の場合で言えば、3つに分けれます。 1つの辺を基準の辺として、延長線を引きます。 その他の三角形の対角線と平行な直線を引き、基準線




從沒見過這麼全的數學圖形計算公式 孩子一看就會 每日頭條
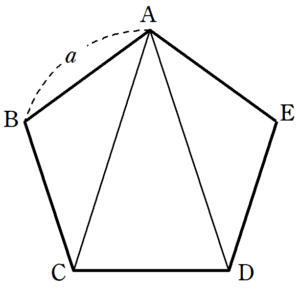
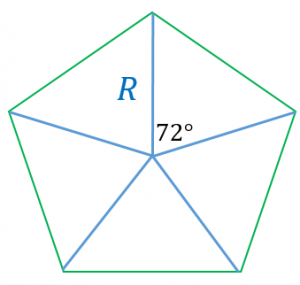
正五角形の面積 中三程度で理解できるように、根号と三平方の定理までを使用し、三角関数は使用していません。 三角関数で解く場合はこちらを参照してください。 1)外接円の半径がわかっているとき 図2の OABの面積がわかれば、それを5倍すればよい。 OBを底辺とすれば、高さは、図3のAHとなる。 ここで、図3の AFOは、∠F=∠O=72°の二等辺三角形である。 図AD = xとすると、比の関係より : : a : x = x − a : a x 2 − a x = a 2 x 2 − a x = a 2 x 2 − a x − a 2 = 0 二次方程式の解の公式より x = a ± a 2 4 a 2 2 = 1 ± 5 2 a x > 0より x = 1 5 2 a これで正五角形の対角線の長さが求められました これを使って、面積を求めていきます 正五角形の面積Sは A B C , A C D , A E D の和であるから角形の内角の和の公式=180×( -2) ※ 絶対に覚えておいて下さい。 例えば 五角形の内角の和=180×(5-2)=180×3=540度 六角形の内角の和=180×(6-2)=180×4=7度 10角形の内角の和=180×(10-2)=180×8=1440度 2 正 角形の1つの内角の大きさを求める! 正三角形の1つの内角の大きさは60度 , 正四角形
正五角形の面積の求め方を小学生でもわかるように説明できますか? 一辺の長さををaとしたときです。 補足 すみません わかりづらく書いてしまったかもしれません。 小学生でもわかるように、というのはできるだけ簡単に、という意味で書いたつもりなのですが。 Ⅰ 面積の公式 以前の記事 · 面積公式 多角形の面積は、頂点の位置ベクトルから 外積 を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを という式になる。 ただし、 とする。 この式を使うと凹多角形でも問題なく計算できるが、自己 · 正三角形の面積、 正五角形の面積 暇なときにでも;
正 n n 角形の面積 1辺の長さが a a である正 n n 角形の面積 Sn S n は、次の公式で求められる Sn = na2 4tan π n S n = n a 2 4 tan 正多角形の面積 1辺の長さが a a である正多角形の面積は、次の公式で求められる 正三角形 = √3 4 a2 正四角形 =a2 正五角形 = √2510√5 4 a2 正六角形 = 3√3 2 a2 正 三 角 形 = 3 4 a 2 · ③ 正五角形 「36°の三角比」より、 \begin{equation} \displaystyle \tan{\frac{\pi}{5}}=\tan{36^{\circ}}=\sqrt{52\sqrt{5}} \end{equation} なので、1辺の長さが \(~a~\) の正五角形の面積は \begin{align} S_5&=\displaystyle \frac{5 \cdot a^2}{4 \cdot \sqrt{52\sqrt{5}}} \\ \\正多角形の面積の公式 一般化 Fukusukeの数学めも 平面図形 面積を求める問題 の基礎 カテキョウブログ 図の斜線部の面積の求め方をおしえてください 正五角形で一辺の長さをaとする Clear 正三角形の円形度の求め方です 4p 面積 周辺囲 2で求めれるみた Yahoo 知恵袋 多角形 四角形 五角形 六角




五边形广告尺寸怎么算 五边形怎么算平方 任意五边形面积公式




最新のhd正五角形面積公式 最高のぬりえ
面積 A = 5 a 2 4 cot π 5 = a 2 4 25 10 5 ≃ 1748 a 2 {\displaystyle A= {\frac {5a^ {2}} {4}}\cot {\frac {\pi } {5}}= {\frac {a^ {2}} {4}} {\sqrt {2510 {\sqrt {5}}}}\simeq 1748a^ {2}} · 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 · 正五角形の面積は 2倍角の公式より あとは三角関数の中身を計算すればよい。 (正五角形の図は下にもあるので適宜参照してください) AB=aとし,AからBEにおろした垂線の足をKとおく。 (つまりKはIHの中点) ∠ABK=36°だから直角三角形ABKにおいて BK



学军小筑 各种图形计算公式 给孩子留着




從沒見過這麼全的數學圖形計算公式 孩子一看就會 每日頭條
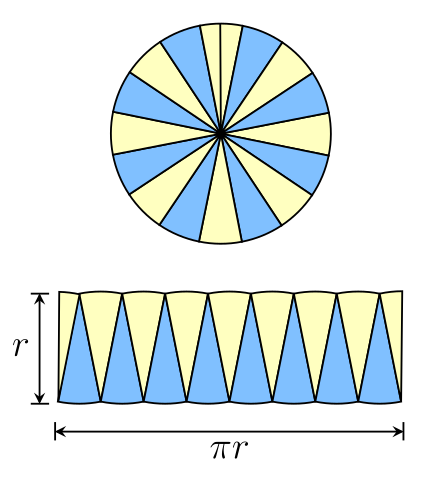
正8角形ですから、図の AOBと合同な二等辺三角形が8個あります。 AOBの面積を求めて8倍すれば良いわけです。 解説 AOBの底辺はRで高さはhであるとし、 hをRで表すことを考える。 45゜ AOHはAH=OHの直角二等辺三角形である。 つまり、辺の比は そこで、 =h となる。 AOB = 2 /4 よって、求める8中2数学正多角形の外角の大きさが3秒でわかる公式 正五角形の外角はすべて等しいので x =360°÷5=72°よって,x =180°-72°=108° 八角形の内角の和は180°×(n-2)よ 角形と言う。 定理(球面三角形の面積の公式) 半径1の球面では、 三角形の面積= 内角の和 ˇ k = 2ˇ 頂点に集まる角の和 多面 · 正多角形の面積から円の面積の公式へ 投稿日:19年10月9日 更新日:19年10月26日 正五角形の面積を求めてみましょう。 抽象的になりますが、一般化を図るために言葉の式で考えます。 次に、正六角形の面積を考えます。 どちらの面積も、 「周りの長さ 高さ÷2」 で求められるようです。 では、正n角形の面積を考えましょう。




Tqc 程式語言python 110 正n邊形面積計算 Jb 程式筆記




六角形面積公式正六邊形面積公式 百度知道翻譯此網頁 Juliech
正五角形の面積を求めるために、形を分解していってる。図にしてみるとこうなる。 これで、イメージはつかめたかな?では、本題に戻ろう。 q6、この正五角形の中で、青い三角形はいくつあるかな。 a5 個。 q7、じゃあ、次に赤い三角形の中は正五角形の中にいくつ含まれている? a 10個 · 正多角形の面積を求めます。 高校数学の問題集に載ってるレベルの問題です。正 角形の1辺の長さを 、重心(正 角形の外心と一致する) o と頂点の距離を (これは外接円の半径でもある)とします: 図中の点 a, b は正 角形の隣り合う頂点、点 m は辺 ab の中点です。 · https//detailchiebukuroyahoocojp/qa/question_detail/q 9 tos******** tos******** さん 12/3/4 1457 正多角形の面積ですね。 下に正五角形の面積の求め方を紹介します。 一辺の長さをa、中心からの距離をrとすると、 5つの三角形の1個分の面積は、 a×r÷2 よって、正五角形の面積は、この5個分なので (a×r÷2)×5 =5a×r÷2 これは、 正五角形の周りの長




利用行列式計算多邊形面積 線代啟示錄




最新のhd正五角形面積公式 最高のぬりえ
四角形・三角形の面積/理解シート 五角形(多角形)の面積を求めるには,どうすればいいの 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author VAIO面積公式推導 正多邊形的面積公式為: = 其中, 是周長、 是邊心距。正五邊形的 和 可由三角函數計算:正十二面体 (面の形は正五角形) 辺の数 5(辺)×12(面)÷2=30 頂点の数 5(点)×12(面)÷3(1頂点を共有する面)= 球の表面積と体積を求める公式を紹介します。 シンプルに 球の表面積 球の体積 の2種類の公式だけです。とても




波提思互動數學教學 正六邊形可化成六個正三角形 上 Youtube




Python 程式設計技巧 Apcs檢測 正五邊形面積為多少
ヘロンの公式 正十二角形の面積 正五角形の面積・正十二面体の体積 正二十面体の体積 数学Ⅱ・B 係数分離法から組立除法へ いろいろな平均 複素平面 共役複素数 虚数の平方根 3次方程式の解と係数の関係 1 · 正 n 角形の面積の公式(n = 3, 4, 5, 6) ちなみに、正三角形〜正六角形までの面積の公式は以下のようになります。 \(\bf{n = 3}\) ( 正三角形 )数学切り抜き帳 正十二面体は,正五角形12枚を貼り合わせてできる多面体である. 付録として正十二面体の 展開図 をつけたのでじっさいに模型を作ってよく観察してもらいたい. 正十二面体をよくみると,じつは, 正十二面体の中には立方体が隠れて
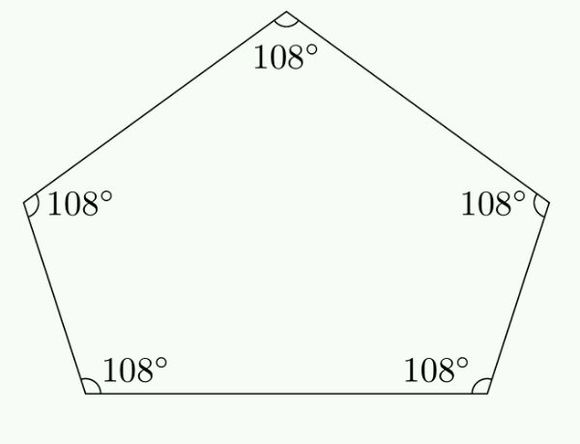



正五邊形 定義 面積公式推導 內切圓半徑 構造 物理方法 畫法 常規畫法 尺規作圖 中文百科全書




3种方法来求五边形的面积
1 使用周长和边心距来计算面积。 边心距是从五边形中心向边作垂线,垂线的长度就是边心距大小。 如果已经知道这个长度,你可以使用下面这个简单的公式。 正五边形的面积= "pa"/2,其中"p" = 周长,"a" = 边心距。 如果不知道周长,可以通过边长来计算。 计算公式是:p = 5s,其中"s"是边长。 {"smallUrl""https\/\/wwwwikihowcom\/images_en\/thumb\/b\/bc\/FindtheAreaofa · 正多角形の面積を考えてみよう(トライさんからの挑戦状) 岐阜県の皆さん、こんにちは。 家庭教師のトライ岐阜本部です。 11月に入り、寒さを感じる季節になってきました。 秋の季節とは関係ありませんが、高校でも、中学校でも、数学の後半は図形十五角形(じゅうごかくけい、pentadecagon)は、多角形の一つで、15本の辺と頂点を持つ図形である。 内角の和は2340°、対角線の本数は90本である。 正十五角形においては、中心角と外角は24 °で、内角は156°となる。 一辺の長さが a の正十五角形の面積Sは = = ( )




最新のhd正五角形面積公式 最高のぬりえ



学军小筑 各种图形计算公式 给孩子留着
正三角形の辺と高さの比、面積 a h= √3 2 a (面積)= 2 √3 4 a 6 方べきの定理(全3 パターン)c pa×pd=pb×pc pa×pd= pb2 pa×pc=pb×pd 7 頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10三角形の面積(3辺からヘロンの公式) 看板の平米数の算出。自分で出した正五角形の面積が正確かどうか確かめたかった。 合ってて良かった。 8 0925 男 / 30歳代 / 会社員・公務員 / 役に立った / 使用目的 建築物の面積・体積の計算 9 1041 男 / 歳代 / 会社員・公務員 / 役Tsoul お礼率 100% (6/6) 一辺をXとした正三角形の面積の 求めかたを教えてください。 それと、一辺をXとした正五角形の 面積の求めかたを教えて




正五角形の長さや面積の導出 数学の偏差値を上げて合格を目指す
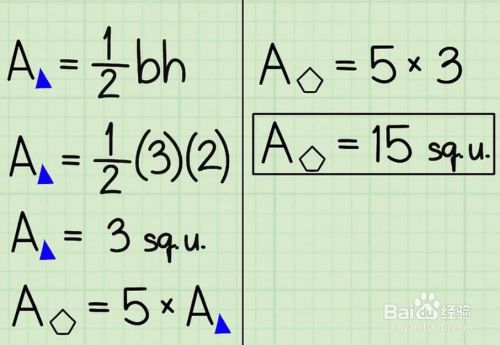



正五边形面积怎么求 百度经验
三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要があるんですね! 忘れないように覚えておきましょう(^^) 三角形の面積を求める問題 それでは、三角形の面積公式を使って問題を解いていき正五角形の面積(東海 04) 図1のように直線上に同じ大きさの正五角形を、 頂点が重なるようにらして並べたとき、 図の色のついた部分の面積は、 同じ大きさの五角形(図2)の①、②の部分の 何個分に相当しますか。 動く解答はこちらをクリック正八角形の中に二等辺三角形が8つ分できてることに気が付きますね。 なので、 二等辺三角形の面積を求めて、それを8つ分にする。 という考え方で正八角形の面積を求めていきます。 中心の360°を8等分していることから




十五邊形 維基百科 自由的百科全書




计算五边形的面积 建议 July 21
(正八边形的)内角 我们也可以用: 如果我们不知道边心距,我们可以用同一个公式,但以半径或者边长为变量: 多边形面积 = ½ × n × 半径 2 × sin(2 × π/n) 多边形面积 = ¼ × n × 边长 2 / tan(π/n) 数值列表 这是不同多边形的边长、边心距和面积的值(半径为 "1"): 种类 名称 (正多边形) 边 · 長方形の面積を求めるために、2つの側面の長さを掛けます All sides of a square are of equal length, and the angles of a square are all right angles 正方形のすべての辺の長さは等しく、角度はすべて直角です The formula for the area of a trapezoid is equal to the half of the sum of the top and base times the height 台形の面積の公式は、上底下底×高さ÷2です




例題 五邊形的五個角度比 Youtube




Fjet9ftd85k9km




正五邊形 正五邊形是指五條長度相等的線段 首尾相連構成的一個封閉形狀且內 百科知識中文網




正八邊形中的等積變換 含原面積 Youtube
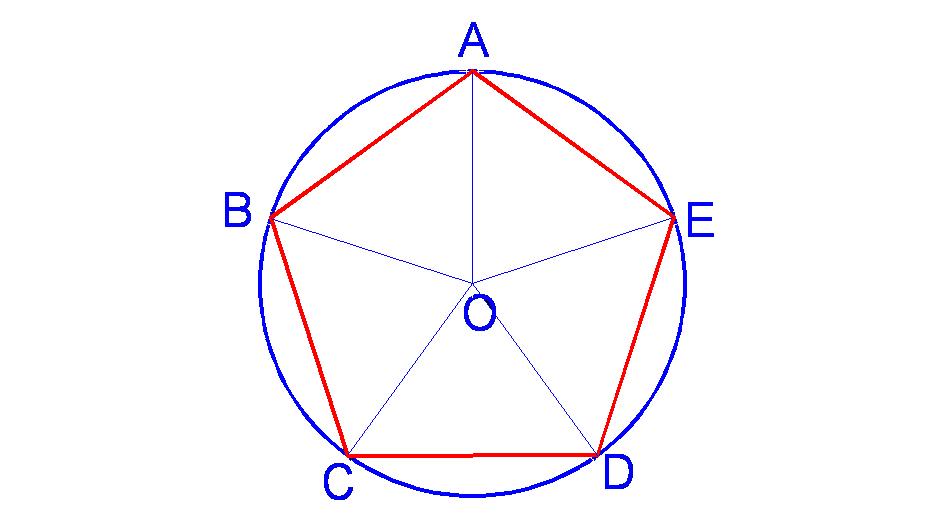



五邊形 完美五邊形 正五邊形 定義 面積 繪製方法 性質 中文百科全書




正多边形 属性




最新のhd正五角形面積公式 最高のぬりえ




画像をダウンロード6角形角度 シモネタ



面積 Wikiwand



數學角落



周长 面积 体积 玄数



小学图形面积公式大全所有阴影面积题有答案 三年级不规则图形面积




3种方法来求五边形的面积



最新のhd正五角形面積公式 最高のぬりえ




3种方法来求五边形的面积




五边形广告尺寸怎么算 五边形怎么算平方 任意五边形面积公式



最新のhd正五角形面積公式 最高のぬりえ



Priori Moe Gov Tw Download Textbook Math Grade8 Book4 Math 8 4 5 Pdf
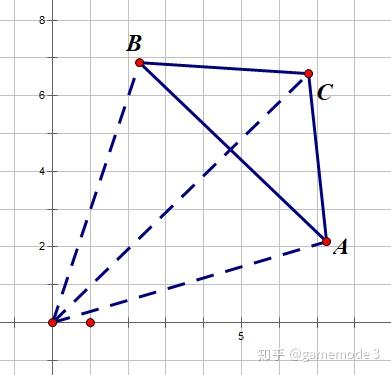



用点坐标求多边形的面积 知乎




國中數學第四冊學習手冊




3种方法来求五边形的面积




3种方法来求五边形的面积




正五边形的外角和是多少度



五边形 维基百科 自由的百科全书




業餘數學家協助解答的難題 怎樣用五邊形來密鋪平面 The News Lens 關鍵評論網



各种图形的计算公式汇总 全给你找好了



正多角形の面積の公式 Fukusukeの数学めも




3种方法来求五边形的面积




最新のhd正五角形面積公式 最高のぬりえ




五边形广告尺寸怎么算 五边形怎么算平方 任意五边形面积公式



Http Web Math Sinica Edu Tw Math Media D361 Pdf




3种方法来求五边形的面积




怎樣用尺規作圓的外切正五邊形 Getit01




Fjet9ftd85k9km



1




正五边形边心距怎么求 知道正五边形边心距怎么算边长 三人行教育网 Www 3rxing Org



1




國中生常考的正五邊形角度問題 Youtube




Python 程式題目演練教材 Online Pages 1 50 Flip Pdf Download Fliphtml5




3种方法来求五边形的面积




Python 程式題目演練教材 Online Pages 1 50 Flip Pdf Download Fliphtml5




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




知識家 單元b 1 幾何 正五邊形 正六邊形面積計算公式 滿意度c 這是個數學愛好者的樂園 歡迎大家都能夠來分享 思考數學題目




最新のhd五角形面積公式



利用行列式計算多邊形面積 線代啟示錄




3种方法来求五边形的面积




最新のhd正五角形面積公式 最高のぬりえ




面積 Wikiwand



正五边形面积怎么求 百度经验




五边形 维基百科 自由的百科全书




九年一貫數學領域綱要研習國中階段的幾何 Ppt Download




正多角形の面積の公式 Fukusukeの数学めも



図形 正五角形の分解 父ちゃんが教えたるっ



Http Science Hsjh Chc Edu Tw Upload Works 106 603bf5ac4dee6efa22ee38d5c0f0cbb5 Pdf




三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下




多角形の内角の和 算数の公式覚えてますか




小三 周長與面積 求正多邊形周長 重點講解 Youtube




最新のhd正五角形面積公式 最高のぬりえ




五边形 Wikiwand



各种图形的计算公式汇总 全给你找好了



正五角形の面積




正五边形计算器



正多边形 圆的周长 圆周率p 玄数




正五邊形與五角星尺規作圖 每日頭條



最新のhd正五角形面積公式 最高のぬりえ




最新のhd正五角形面積公式 最高のぬりえ




五边形 维基百科 自由的百科全书




计算五边形的面积 建议 July 21




最新のhd正五角形面積公式 最高のぬりえ



正多边形 圆的周长 圆周率p 玄数
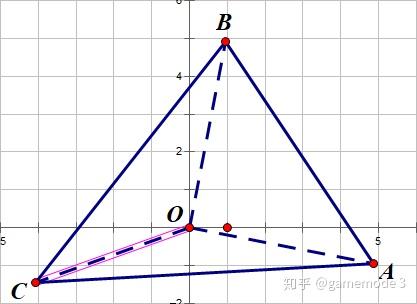



用点坐标求多边形的面积 知乎




圓內接正五邊形 內接於圓的正五邊形是圓內接正五邊形 圓內接正五邊形性質 百科知識中文網



1




五边形 维基百科 自由的百科全书




3种方法来求五边形的面积




五边形 维基百科 自由的百科全书



1




正五边形 搜狗百科
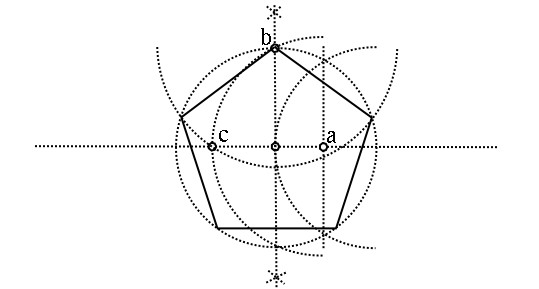



五邊形 完美五邊形 正五邊形 定義 面積 繪製方法 性質 中文百科全書



小学图形面积公式大全所有阴影面积题有答案 三年级不规则图形面积



Http Web Math Sinica Edu Tw Math Media D364 Pdf




计算五边形的面积 建议 July 21




正五邊形 正五邊形是指五條長度相等的線段 首尾相連構成的一個封閉形狀且內 百科知識中文網




基測數學 094v2 單選25 六邊形面積 Youtube



正十二面体面积计算 研发埠 Www Yanfabu Com
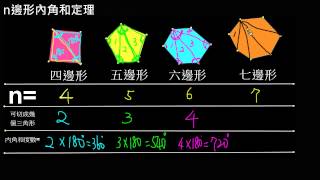



N邊形內角和定理 Youtube



0 件のコメント:
コメントを投稿