/10/16 · 1:高校受験数学の問題で、四角柱の頭部を切断した残り部分の体積を求める公式として 底面積x (abcd)/4(abcdはそれぞれ底面に垂直な辺の長さ) · 四角柱の体積=底面積×高さ =(台形の面積)×高さ = {(上底下底)×高さ÷2}×高さ となります。 つまり {(2+4)×2÷2}×3 =18㎤ この問題の答えは18㎤ということになります。 他の四角形の面積についても、これを機に復習してみてはいかがでしょうか。A B C D O 15cm 12cm 底面が1辺12cmの正方形で、他の辺が15cmの正四角錐OABCDの体積を求めよ。 A B C D O 15cm 12cm O A C 15cm 15cm D A B C 12cm 12cm 点O,A,Cを通る平面で切断する。 切断面の OACは二等辺三角形
1 1 負數與數線
正四 角柱 体積
正四 角柱 体積-表面積 一辺を とすると = ()切頂四面体(せっちょうしめんたい、英 truncated tetrahedron )、または切頭四面体(せっとうしめんたい)、切隅四面体(せつぐうしめんたい)、角切り四面体(かくぎりしめんたい)とは、半正多面体の一種で、正四面体の各頂点を切り落とした立体である。




トップ100 角錐台体積
· 先がとんがっている立体の体積の計算は「底面積×高さ×1/3」になる って覚えておけば問題ないよ。 だから例題の正四角錐の体積は、 6×6×8×1/3 = 96 cm³ になるんだ。 おめでとう! これで正四角錐の体積を計算できたね^^12面体を小立方体とその各面に正四角錐を貼り付けたものとして考えます。 小立方体の1辺=元の立方体の1辺8cm。 小立方体の体積512cm 3 。 正四角錐の底面:1辺8cm、高さ4cm。 正四角錐の体積256/3cm 3 。 よって、12面体の体積 =小立方体+正四角錐 =512+512また、底面が正多角形で、側面がすべて合同な二等辺三角形である角錐を正角錐といいます。角柱とは異な り、底面が正多角形であっても正角錐とはならない角錐があるので注意をしましょう。 ⃝1 正三角錐(正四面体) 正三角形 ⃝2 三角錐(正三角錐で
切頂四面体(せっちょうしめんたい、英 truncated tetrahedron )、または切頭四面体(せっとうしめんたい)、切隅四面体(せつぐうしめんたい)、角切り四面体(かくぎりしめんたい)とは、半正多面体の一種で、正四面体の各頂点を切り落とした立体である。図1.正四角錐の作り方 (2) 正四面体 この正四角錐には底がない。しかし、正四面体にすると、底ができる。 作り方(図2):正四角錐の側面で、厚さが最も薄い側面に折り目を付ける(左図)。内側に折 り込んで、のりを付けて三角錐にする。正多面体 表面が、平面や円状、球状などを含む \(3\) 次元の空間的な広がりをもつ物体を立体といい、立方体、角柱、円錐、球などがあげられます。そのうち、 \(4\) つ以上の平面だけで囲まれた立体を 多面体 (ためんたい) といいます。 三角形や四角形のように、\(1\) つではなく〈多〉くの
· よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式! ? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、対角線などの長さ/錐や柱の体積など/立体上の2 点の距離/角柱・角錐の最短距離/ 円錐・円柱の最短距離 /立体→切断面の平面図形断面が二等辺三角形など/ 断面がその他の三角形/ 断面が四角形/円柱・球など/体積正四面体/体積:高さの発見/いろいろな立体/正多面体/展開図/空間における平面と直線/回転体など/投影図/ 角柱・角錐の表面積 /円柱の表面積/円錐の表面積/柱の体積/錐の体積/立体の切断など 球の表面積・体積/ FdData 中間期末製品版のご案内




50 素晴らしい角錐体積公式 ページを着色するだけ




1 A 6pp12 Q Qpqp8 Ab1bc1 Descubre Como Resolverlo En Qanda
正方形 四 角錐 の 体積 私は正四角錐の体積を求めて4つの三角錐 4で球までの長さをxにして解いたのですが答え Clear 正6面体の中の正8面体の体積の求め方 中学1年数学 空間図形 角柱 円柱の表面積と体積の公式 数学fun 体積について 図のように立方体の1いろいろな立体の問題 第2節 立体の回転体の体積(その1) ここでは,立体を回転したときの体積を求めます.直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積
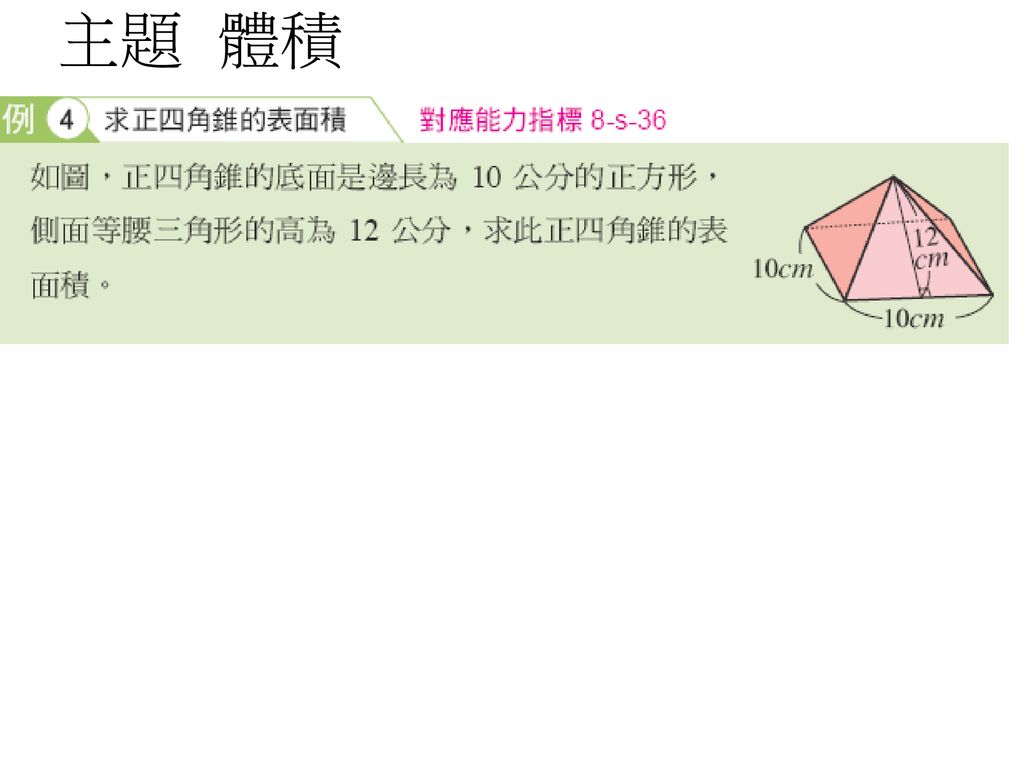



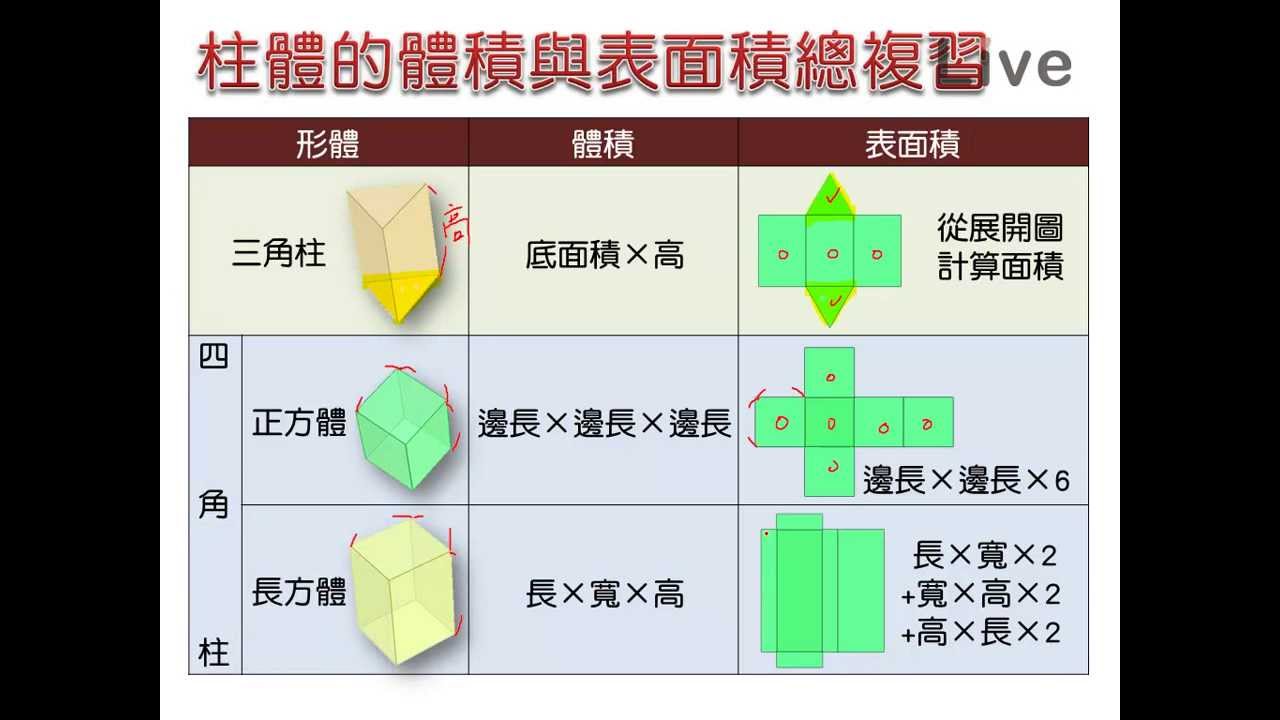
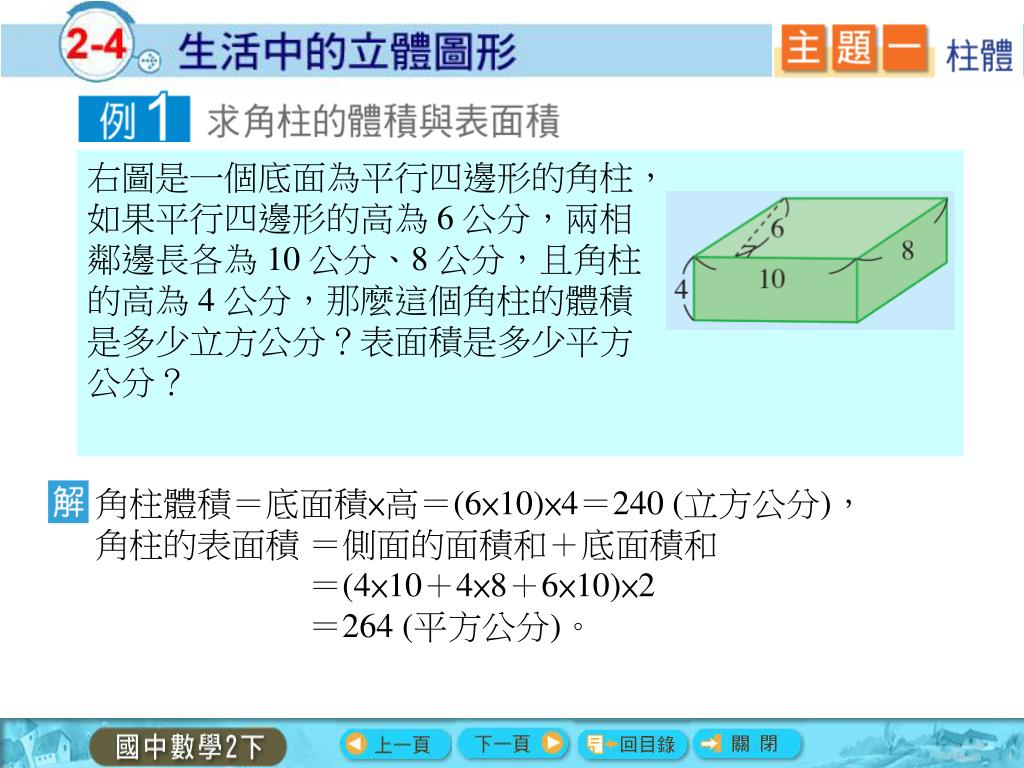
2 4 生活中的立體圖形能以最少性質辨認立體圖形 能理解柱體 錐體的頂點 面 邊的組合因素 能理解柱體 錐體的基本展開圖 Ppt Download




六角錐六角錐數 Yzkgo
/02/11 · 角柱と円柱の底面積と体積の求め方を教えて下さい 4角柱⤵︎⤵︎⤵︎ ①体積が105cm3で、高さが6cm4角柱の体積は何cmですか。 式 答え ⤵︎⤵︎⤵︎円柱 ②体積が945cm3で、底面積が785cm2の円柱の高さは何cmですか。 式 答え · 正三角柱とは、正三角形を底面とし、側面は合同な3つの長方形(または正方形)で構成された立体です。 rsqupyramidカスタムワークシート関数群は、正四角錐の体積や表面積などを計算します。正四角錐とは、正方形と合同な4つの三角形で構成された出典 フリー百科事典『ウィキペディア(Wikipedia)』 正三角錐柱 (せいさんかくすいちゅう、 Elongated triangular pyramid )とは、7番目の ジョンソンの立体 で、正三角柱の内の1つの底面に 正三角錐 ( 正四面体 )をつけたものである。




四角柱 维基百科 自由的百科全书



四角柱 维基百科 自由的百科全书
· 四角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。 よって、計算は次のようになります。正六角柱の体積 高精度計算サイト 計算公式正四角錐の体積の求め方がわかる3ステップ 立体の体積の求め方。何角柱でも何角錐でも同じ! 正四角柱の体積の求め方はなんですか? 正四角 教えて!goo 正四角錐台の体積 高精度計算サイト 3分で正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積




Bar7 1 6cm 8cm A 6cm Descubre Como Resolverlo En Qanda




この問題の解き方を教えてください お願いします Clear
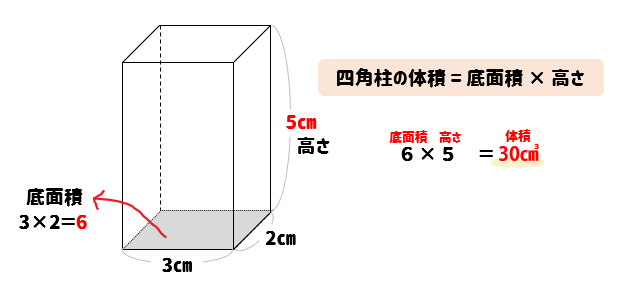
三角柱や四角柱などの体積は、底面積 $S$、高さ $h$ として、次の式で求められます。 角柱 (かくちゅう) の体積 \begin{align*} V = Sh \end{align*} 体積 = 底面積 × 高さ小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント 小学6年生の算数角柱や円柱の体積の求め方・公式の練習問題プリントを無料ダウンロード・印刷七面体(しちめんたい、ななめんたい、英 heptahedron )とは、7つの面からなる多面体である。 五角柱や六角錐は多くの人が知る七面体であるが、七面体は他にも様々な形状のものがあり、凸七面体だけでも34種類のトポロジー的に異なるものが存在する 。
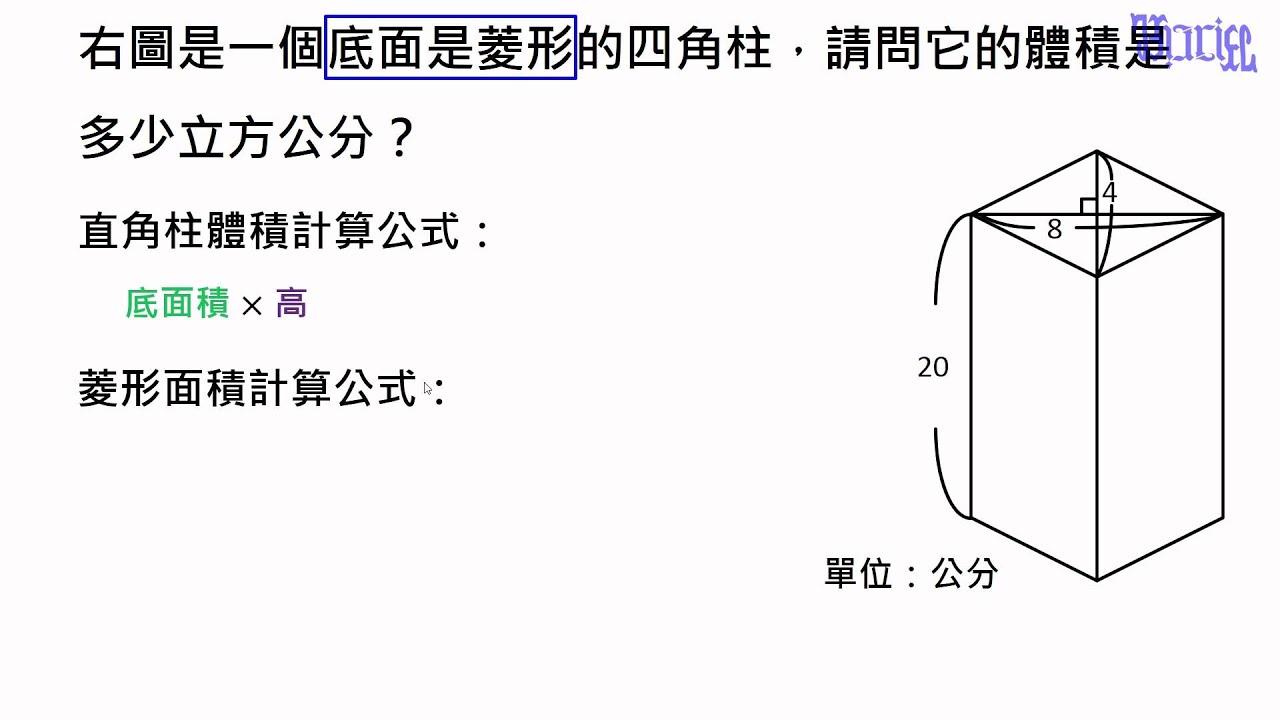



上四角柱表面積 最高のぬりえ




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
· 三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。 · 正六角柱 単独での 空間充填 が可能であるため 平行多面体 である。 体積 Vは、 柱体 の 体積 が底面積×高さである事により、底面の一辺の長さをa、高さをhとすると V = 3 3 2 a 2 h {\displaystyle V={\frac {3{\sqrt {3}}}{2}}a^{2}h} で求まる。体積計算 byNSDev 計算結果は選択コピーして他のアプリで使用できます。 電卓と同じようなメモリ機能があります。 メモリ内容もコピーして他のアプリで使用できます。 1体積を計算する形状を選択します。 2入力項目に入力します。 3 計算開始




はどうやって求めますか 問題が全然わかりません 解説お願いします Clear



1 1 負數與數線
· 正四面体の内接球の半径 この公式の応用例として,1辺が a a a の正四面体の内接球の半径を求めてみます。入試問題で頻出です。 正四面体の表面積と体積は公式として覚えておくとよいでしょう。 →正三角形の面積,正四面体の体積 · なぜ角錐や円錐の体積は3分の1になるんでしょうか。 中1にもわかるように、お願いします! 立方体が6つの面のそれぞれを底面とし,高さが立方体の1辺の長さの半分である合同な6つの四角錐に分割できるということはよいで · 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。




四角柱 Wikiwand
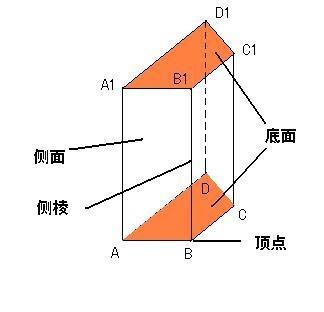



四棱柱 搜狗百科
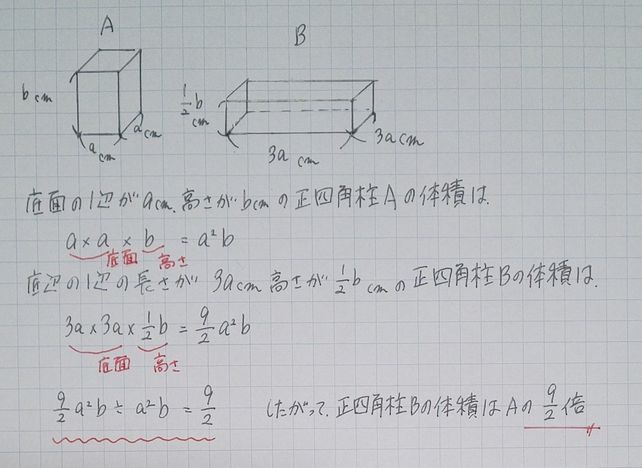
正四面体 内接球 外接球 内接球 外接球 内接球 外接球 内接球 直円錐 正四角錘 三角柱 a a a a a b b b b b h h h h h m m c c c c c d d e b m h n c d e o o o o o o o 球の半径 r は abcの内接円 の半径となるので 球の半径 r は abcの 外接円の半径となるので 正弦定理より求める正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積正四角錐の底面が正四角形です。底辺の長さ (a) が等しいです。縦辺の長さ (b) も同等です。側面が二等辺の三角形です。正角錐の高さの基点が底面の中心と一致します (O) 。 角錐の側の面が側面を形成します。正四角錐の場合は、側面が二等辺の三角形です。
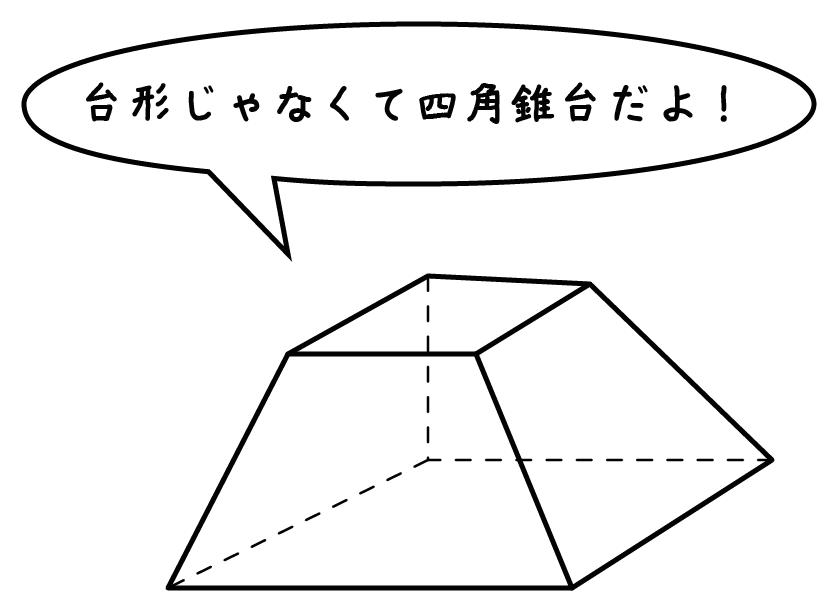



トップ100 角錐台体積
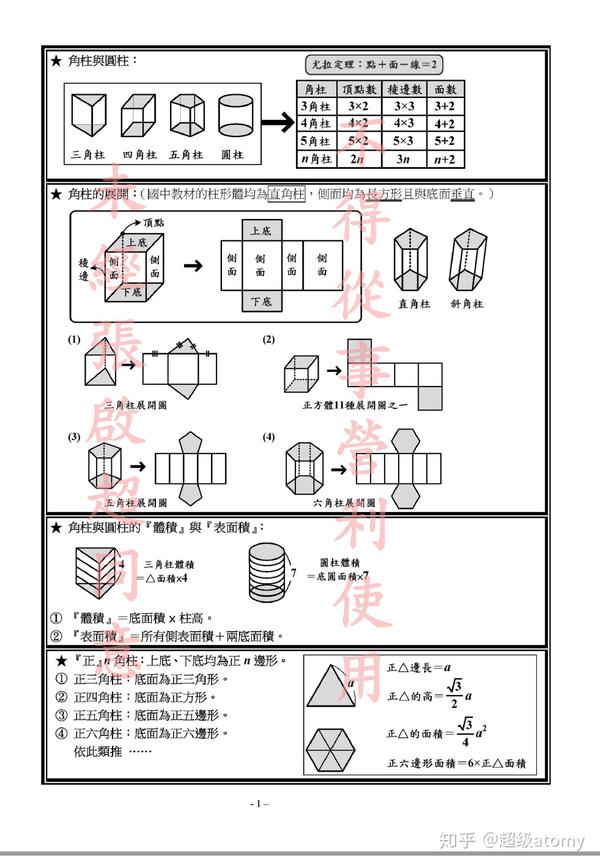



初中数学万题 讲义 详解 Pdf 百度一下阿超数学 知乎
(正五角柱の体積S):(五角錐の体積T)= 5 a : a 3 2 = 5 : 3 2 =15:2 問題 右の図のように,立方体の底面の各辺の中点と,この面と向かい 合う面の対角線の交点を結ぶと正四角錐ができる。このとき,正四 角錐の体積は,立方体の体積の何倍になるかを五角錐(ごかくすい、英 pentagonal pyramid )とは、底面が五角形の角錐である。 特に底面が正五角形で、頭頂点から底面に下ろした垂線が底面の中心で交わるものを正五角錐といい、その側面は二等辺三角形である。 正五角錐の内、側面が正三角形のものは2番目のジョンソンの立体である。Projection of x onto 3D lines;




角錐體積公式的由來 Youtube




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積正三角錐柱(せいさんかくすいちゅう、Elongated triangular pyramid)とは、7番目のジョンソンの立体で、正三角柱の内の1つの底面に正三角錐(正四面体)をつけたものである。 性質 辺構成 正三角形同士が接する:3、正三角形と正方形:33、正方形同士:3;




トップ100 角錐台体積



Math 容器にものを入れる問題 公式 体積 底面積 高さ の応用 働きアリ



正十二面体体积推导补 信息图文欣赏 信息村 K0w0m Com



四角錐 维基百科 自由的百科全书



50 素晴らしい角錐体積公式 ページを着色するだけ



1




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
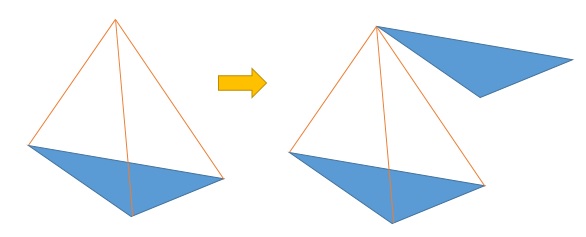



鈄截柱體體積 Quod Erat Demonstrandum




正四角錐3つから正四角柱1つがつくれる 中1 空間図形の体積 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles




四角柱 维基百科 自由的百科全书




四角柱体積公式 犬イラスト
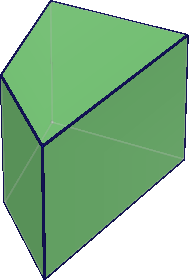



四角柱 Wikiwand



Www Sdime Ntnu Edu Tw Uploads Asset Data 5dfad41c E9 96 B1 E8 Ae 80 E4 B9 9d E4 B8 8b E7 Ac Ac E4 Ba 8c E7 Ab A0 E5 85 A8 Pdf



1




棱柱的表面积体积公式 求四棱柱的表面积和体积公式 三人行教育网 Www 3rxing Org




正四稜柱 上 下底面都是正方形 且側棱垂直於底面的稜柱叫做正四稜柱 正四 百科知識中文網




600cm3 10cm See How To Solve It At Qanda




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




鈄截柱體體積 Quod Erat Demonstrandum




正四角柱から正四角錐へ Geogebra




中学数学 四角柱 Youtube




立體圖形 Geogebra



1



长方体是什么 关于长方体的详细介绍 创闻头条



Http Www Goodschool Com Tw Doc Www Goodschool Com Tw Concept Pdf



Ppt 除了平面圖形以外 像下列這些在生活中常見物體的形狀都是立體圖形 Powerpoint Presentation Id




四角柱 维基百科 自由的百科全书




R H A A See How To Solve It At Qanda




上四角柱表面積 最高のぬりえ



1 1 負數與數線



大嘴鳥親子雜誌




600cm3 10cm See How To Solve It At Qanda



この問題で 正四角錐と正四角柱の体積が正しいからと言って 何故 正四角錐 Yahoo 知恵袋
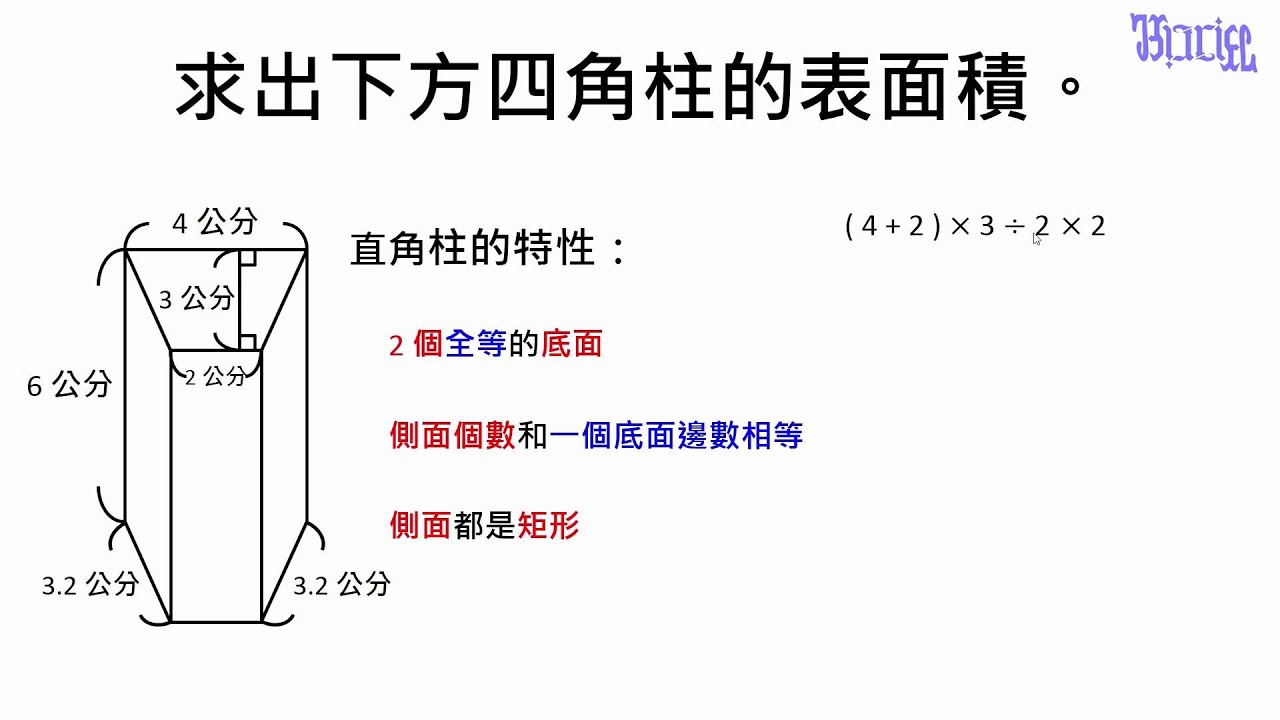



柱體的體積與表面積 04 求出四角柱的表面積 Youtube




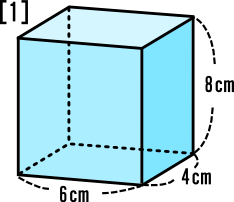
四角柱の体積と表面積の求め方



1
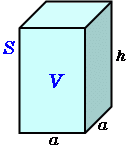



正四角柱の体積 高精度計算サイト




四角柱の体積と表面積の求め方
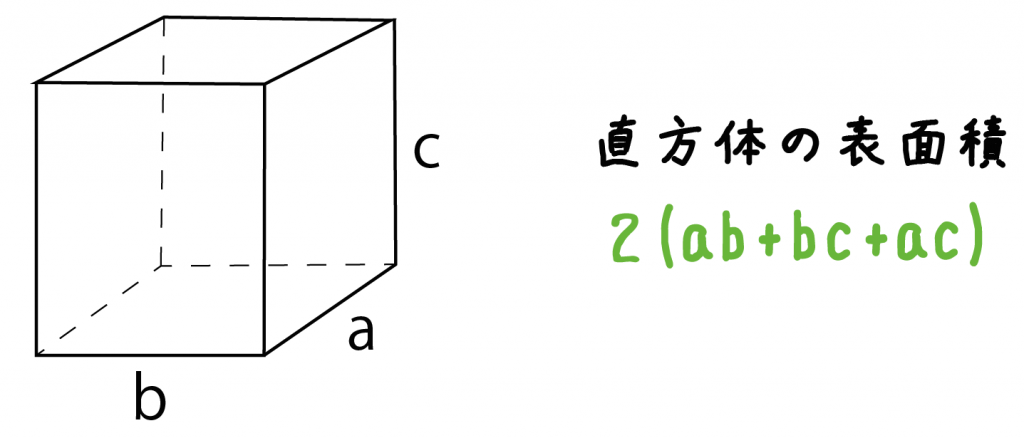



上四角柱表面積 最高のぬりえ




长方体 Wikiwand




四角柱 维基百科 自由的百科全书
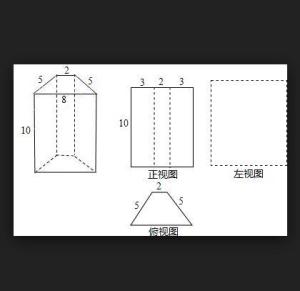



四棱柱 搜狗百科




立體圖形 授課篇 適用年級 5 6年級設計者 Mri團隊 Ppt Download




四角柱 Wikiwand



1 1 負數與數線




四角錐台の体積 高精度計算サイト




4 1 Acm Descubre Como Resolverlo En Qanda




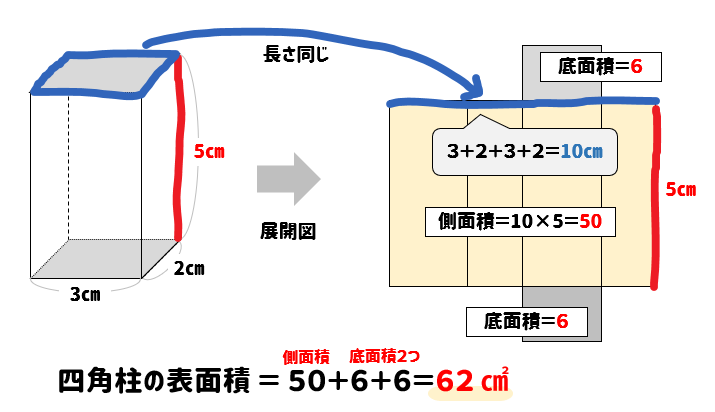
3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




四角柱 维基百科 自由的百科全书



数学の問題で分からないところがあります 体積の等しい正四角錐 Yahoo 知恵袋




小園丁 台灣製益智教具 十形容器展開圖 露天拍賣




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Ppt 除了平面圖形以外 像下列這些在生活中常見物體的形狀都是立體圖形 Powerpoint Presentation Id



1 1 負數與數線



长方体是什么 关于长方体的详细介绍 创闻头条



長方體 维基百科 自由的百科全书



Http Jendo Org Files 6year E6 95 99 E5 Ad B8 E8 87 E6 Ba 90 E6 95 B8 E5 Ad B8 E5 87 E4 B8 E8 92 E9 8c 90 A113 Pdf
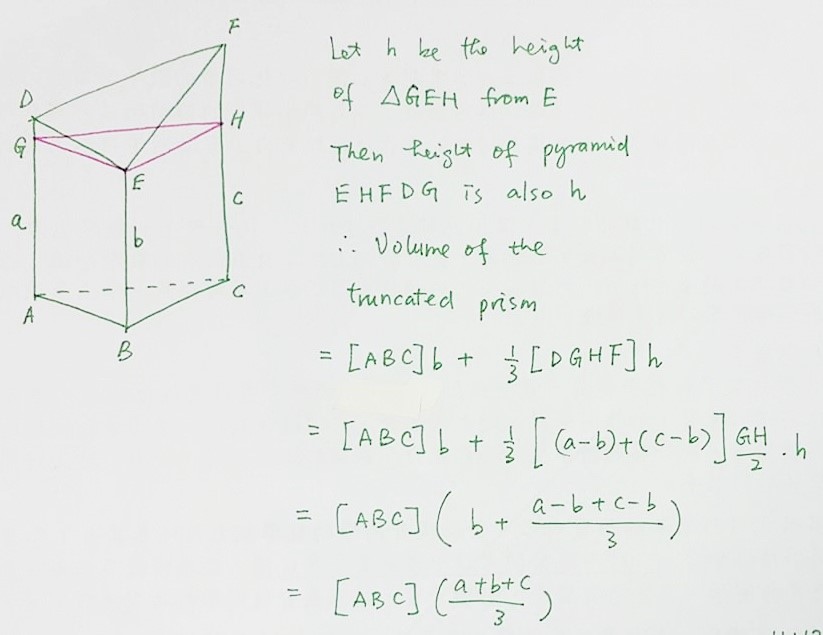



鈄截柱體體積 Quod Erat Demonstrandum
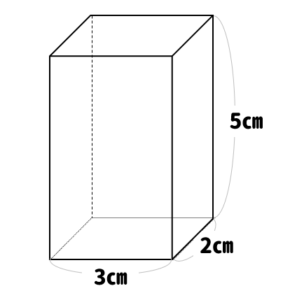



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



Http Www Goodschool Com Tw Doc Www Goodschool Com Tw Concept Pdf




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット



如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌



Http Www Gjjh Tp Edu Tw Mediafile Fdownload 69 446 16 2 29 22 0 43 446 Nf1 Pdf




7 1 Acm Hcm A A Left O3 Sor See How To Solve It At Qanda




鈄截柱體體積 Quod Erat Demonstrandum




梯形体体积计算公式与在线计算器 三贝计算网 23bei Com




体積の求め方 計算公式一覧



正四角柱の体積の公式ってなんでしたっけ どうしても思い出せませんどなたか教え Yahoo 知恵袋




エレガント四 角柱 の 体積 最高のぬりえ




求三棱柱的体积和表面积 三棱柱的表面积公式和体积公式 三人行教育网 Www 3rxing Org



上四角柱表面積 最高のぬりえ




1 Boy的聲音問 Ppt Download



2




Sqrtsqrt12 1a Cm Hcm Descubre Como Resolverlo En Qanda




立體圖形 授課篇 適用年級 5 6年級設計者 Mri團隊 Ppt Download



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ



大嘴鳥親子雜誌



Http Jendo Org Files 6year E6 95 99 E5 Ad B8 E8 87 E6 Ba 90 E6 95 B8 E5 Ad B8 E5 87 E4 B8 E8 92 E9 8c 90 A113 Pdf




四角柱 Wikiwand




四角柱 Wikiwand




61 1 2 10cm10 Cm6 Cm6 Descubre Como Resolverlo En Qanda




四稜柱 在幾何學中 四角柱又稱四稜柱 是指底面為四邊形的柱體 當底面為正 百科知識中文網



长方体是什么 关于长方体的详细介绍 创闻头条



4 1 Acm Descubre Como Resolverlo En Qanda



0 件のコメント:
コメントを投稿