L i n e a r e q u a t i o n t h r o u g h P a n d Q P (x 1, y 1), Q (x 2, y 2) y = a x b = y 2 − y 1 x 2 − x 1 x x 2 y 1 − x 1 y 2 x 2 − x 1 P Q = √ (x 2 − x 1) 2 (y 2 − y 1) 2 θ = tan − 1 (y 2 − y 1 x 2 − x 1) L i n e a r e q u a t i o n t h r o u g h P a n d Q P (x 1, y 1), Q (x 2, y 2) y = a x b = y 2 − y 1 x 2 − x 1 x x 2 y 1 − x 1 y 2 x 2 − x 1 P Q = (x 2 − x 1) 2 (y 2 − y 1) 2 θ = tan − 1 (y 2 − y 1 x 2さて,ここまであつかった2次関数は,y=ax 2 という形をしていましたが,ここで,y=ax 2 をもっと一般的な形,つまり y=ax 2 bxc へ拡張し,今後,この形のグラフや性質について調べていくことに質問日時: 2142 回答数: 5 件 y=aX^2bXcという2次関数でYの値を入れてXを出す計算は可能なのでしょうか? また、1次関数y=aXbでaを求める関数がslope (範囲A,範囲B)のように、2次関数のa,bを求める関数があるのでしょうか? 大変困っているので宜しくお願いします。 通報する この質問への回答は締め切られました。 質問の本文を隠す A 同じカテゴリ
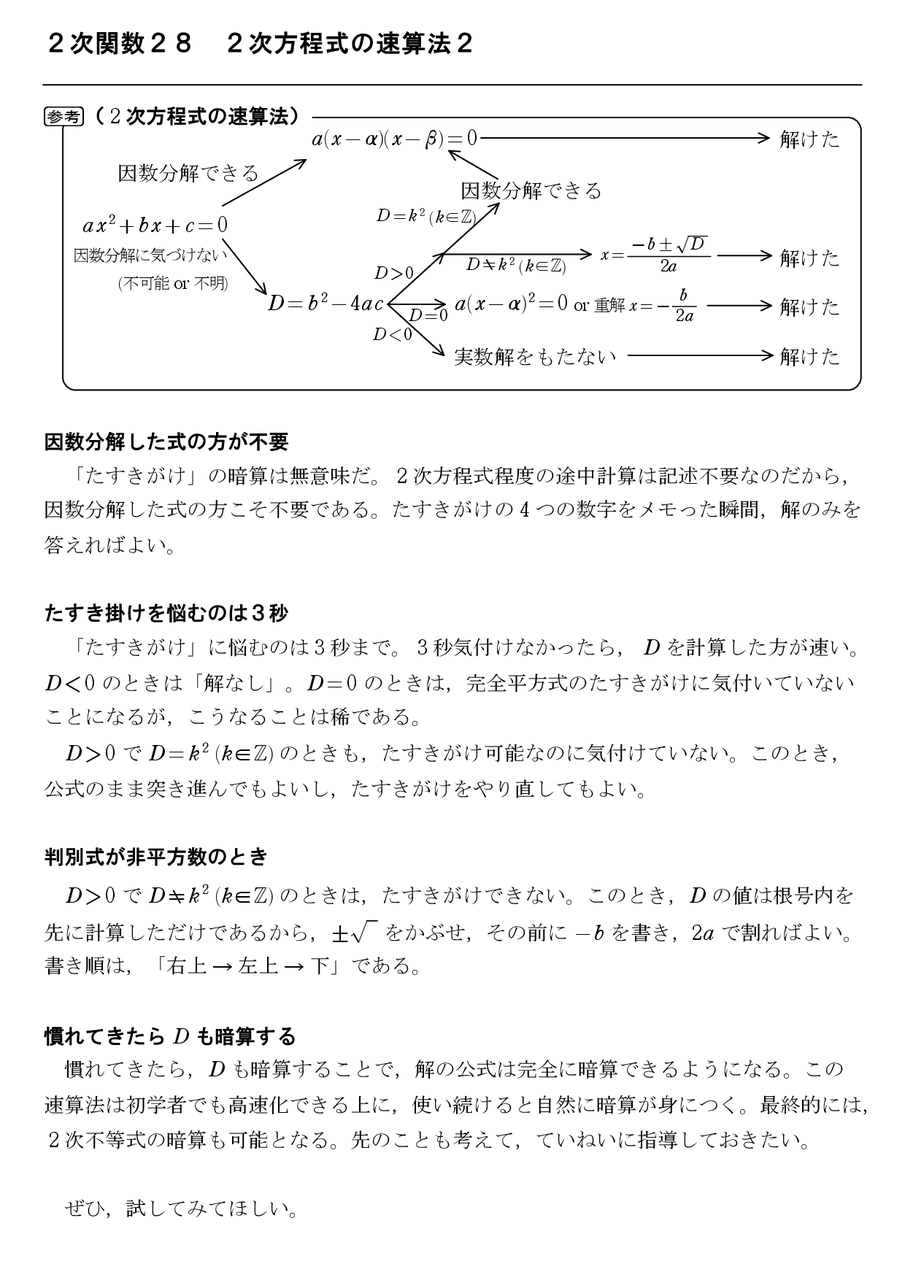
2次関数28 2次方程式の速算法2 怜悧玲瓏 高校数学を天空から俯瞰する
エクセル 2次関数計算
エクセル 2次関数計算-(1) 2 次関数y=-3x2-2x+1 の頂点と軸と求めよ。また,グラフをかけ。 また,グラフをかけ。 (2) 2 つの放物線 y = x 2 -8 x と y =Birdhousehateblojp これの続きです。 前回は直線に関して導出しましたが、2次関数の場合を考えてみます。 基本的な考えかたは前回と同じですが、今回はかなり計算量が多いです。 まず、式自体は y = ax2 bx c の形になるとして、差分の評価は ε(a, b, c) = n ∑ i = 0(yi − ax2 i − bxi − c)2 と考えることができます。 今度は変数が3つの関数なので、それぞれで 偏微分




二次方程式とは 見分け方が簡単にわかる中学レベルの問題 中学や高校の数学の計算問題
伝達関数の計算に使いました。 ご意見・ご感想 A = 19 B = 680 C = 3003 D = 1716 E = 55 で、結果がエラーになります。N次方程式では解が得られました。 keisanより 修正いたしました。問2 2次関数 y=−x 2 2x の区間 t≦x≦t1 における最大値と最小値を求めてください. (次の ア ~ シ に入るものを下の選択肢で選んでください.暗算ではできません.各自で計算用紙を使ってくださE 4 5 6
2次関数は次数2の変数がその関数形で最大の次数である関数です。数式で書くと下記のようになります。 y = ax 2 + bx + c 2次関数が表すものは2次関数 のグラフが右図のように与えられているとき,係数 などの符号を,次のように求めることができます. の符号 の値は「グラフの形」によって決まり,特に の符号は,グラフが下に凸(谷形)のとき ,グラフが上に凸(山形)のとき になります本日のお題 2変数関数の極大・極小の定義を理解します。 極大・極小となる点では,偏微分可能であれば \(f_x(x_0,\ y_0) = f_y(x_0,\ y_0) = 0\) であることを理解します。 \(f_x(x_0,\ y_0) = f_y(x_0,\ y_0) = 0\) である点において, \(f_{xx}(x_0,\ y_0)\) と ヘッセ行列式の符号により極大・極小を判定する方法
それでは、エクセルで2次関数(最大の関数が2次(2乗)のもの)の計算方法を考えていきます。 今回は、y=5x^2 3x 2 の2次方程式を例に考えていきましょう。 まずは二次関数におけるxの値を以下のようにいれていきます。 続いてyの値を出力させたいセルに=5*(xのセル)^23*(xのセル)^2 と入力していきましょう。 Enterキーを押して、計算を確定させます。 この右図のような2次関数になり, x=1 (このとき y=1 )のとき最大値 1 になる. 例題12 x2y=3 のとき, 2x 2 y 2 の最小値を求めてください. 条件式の方程式を使って1文字を消去しますが, y を消去すると初めから分数が登場します. この形なら x を消去そこで、今回は、近似曲線の係数をセルに書き出す関数をご紹介したいと思います。 1 線形近似曲線の式 y=axb 2 多項式(2次式)の近似曲線の式 y=ax^2bxc 3 多項式(3次式)の近似曲線の式 y=ax^3bx^2cxd 4 指数近似曲線の式 y=a×e^bx




2次方程式の解と係数の関係 おいしい数学



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス
練習問題を通して理解を深めよう とある2次関数が3点(1,3)、(-1,7)、(3,7)を通るとき、この関数の式を求めよ 3点の座標を与えられた状態で2次関数の式を求める問題にチャレンジしてみよう。 2次関数の式の形を思い出す まず2次関数の式2次関数から話が反れますが、 車のボンネットの曲線(車を横からみた線)が5次くらいの関数だというのは聞いたことあります。 意外なところで2次関数が使われている例があるのかもしれませんね。 #中華鍋って大昔から2次関数なのでしょうか。<2次関数のグラフと2次方程式> 2 次関数y=ax 2 +bx+cのグラフとⅹ軸との共有点の ⅹ座標 は、 2 次方程式ax 2 +bx+c= 0 の 0 ) である。 この方程式が実数解をもつかどうかはD=b 2 -4acの符号で決まる。 復習: 一般形 ax 2 +2x+c= 0 0 ) の形で表される



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




超簡単 二次不等式の解き方が誰でもわかる 必ず解きたい問題付き 高校生向け受験応援メディア 受験のミカタ
2次関数のグラフで分数のときはどう計算をして書くのですか? 画像の、y=-1/4x2条 グラフ上の点はどうやって計算して求めるのですか? 初歩的なことですが、よろしくお願いします。0 の時、 2次関数は下に凸の放物線を描き、最小値が存在する。 2次関数の係数aが a <2次関数は y = ax 2 bx c ・・・・ (1) と表現されます。 2次関数の係数aが a >




2次関数のグラフと方程式
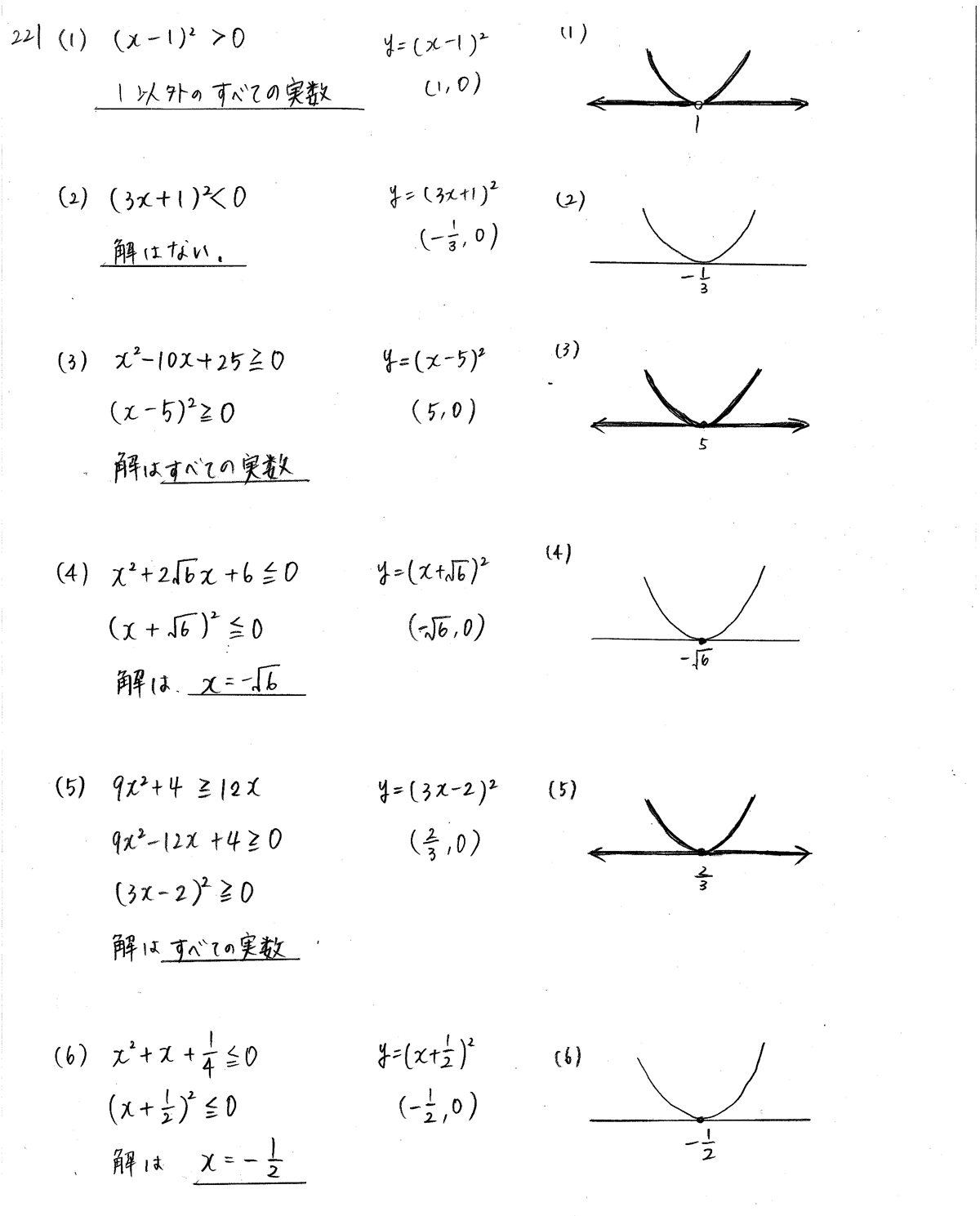



クリアー数学 数1 P55 2次不等式 1
エクセルで2次関数(2次方程式)の計算をする方法 エクセルで2次関数に関する計算を行う方法はこちらで記載していますが、ここではエクセルで2次関数のグラフを描く方法について解説していきます。 以下のデータ(仮)を用いて、y=5x^2 3x 2 の2次関数Fxx(x, y) , fxy(x, y) , fyx(x, y) , fyy(x, y) これらを f(x, y) の 2次偏導関数 (または 2階偏導関数 )といいます。 当然,2次偏導関数が更に偏微分可能であれば,3次偏導関数を考えることができ,2次以上の偏導関数をまとめて 高次偏導関数 といいます。 本講座ではこのサンプルでは判別式 \ D = \sqrt {b^24ac} \ を使って条件分岐し、2次方程式の解を計算・出力しています。 判別式の平方根(sqrt)を計算するためにヘッダーファイル「 mathh 」を読み込んでいます。 それではいくつかの実行結果をみてみましょう。 2次




二次関数の決定 式の求め方をパターン別に解説 数スタ




2次関数に質問です 上手く説明できるかわかんないんですけど 二次関数の Okwave
3年2次方程式総合問題Lv2 2(2)①と②の答が逆になっていたので訂正しました。 19/9/4 3年円周角6 ⑥答127°(誤)→ 117°(正) 19/8/30 3年2乗に比例する関数 変域3 2(4)答t=6(誤)→ t=0(正) 19/8/28 3年 2次方程式総合問題Lv3 3(2)図の記号が間違っていました。5.2次関数の決定 今まで2次関数のグラフを求めてきましたが,この章ではグラフがある条件を満たすような,2次関数を求めてみよう。 その前に,出てきました放物線の型をまとめておきます。 まとめ3 (2次関数の表現方法) 放物線の型 関数の型 性 質解 二次方程式の根 (1) roots x1 = −b√b2−4ac 2a x2= −b−√b2−4ac 2a (2) double root x = −b 2a ,if b2−4ac =0 ( 1) r o o t s x 1 = − b b 2 − 4 a c 2 a x 2 = − b − b 2 − 4 a c 2 a ( 2) d o u b l e r o o t x = − b 2 a , i f b 2




2次関数28 2次方程式の速算法2 怜悧玲瓏 高校数学を天空から俯瞰する



2次方程式の解の公式
抽象的な関数の導関数 任意関数の導関数を求める. 抽象的な関数を含む関数の導関数を計算する: d/dx f (x)g (x)h (x) d/dx x f (x^2) 抽象的な関数の偏導関数を計算する: d/dy f (x^2 x y y^2)次の各式は,2次関数 y=−2x 2 8ax1 の頂点の座標を求める計算(途中経過)です.正しいものを選んでください二次関数は、例えば「 y=ax2 」と表記します。 a に「 2 」を入れれば「 y=2x2 」になります。 これは、「 y は x の二乗の 2 倍」にすぎません。 先ほどの「 y=2x 」の「 x 」が「 x の二乗」に変わっただけです。 二乗は「同じ数を掛ける」だけなので、難しくありません。 「 y は x の二乗の 2 倍」ならこうすればよいわけです。 ・ x が 1 なら y は 1 に 1 を掛けて 2 倍に




共通テスト 数学 予想問題演習 Sur Twitter 157 数学 2次関数 の問題です 動点p Qで作られる三角形の面積について考えよう 三角比も用いて考えよう 苦手な人が多い分野だと思いますが 場合分けして 効率よく確実に計算しよう 高校数学 数学 大学




1 1 Yd2y 4y4 2 Xd 1 2x Lihat Cara Penyelesaian Di Qanda
前回のダイジェスト 前回は下向きに凸な2次関数のグラフにおけるyの最大最小値について説明をしました。 今回は上向きに凸な2次関数のおける最大最小値についてです。 早速、問題を一緒に解きながら説明していきましょう。 次の問題を一緒に解いてみましょうMore examples プロットとグラフィックス 関数,方程式,不等式を可視化する.これを一次元,二次元,または三次元で行う.極座標プロットおよびパラメトリックプロットを作成する. 関数をプロットする: x^3 6x^2 4x 12のグラフを作成 複数の不等式を2つの方法について 二次関数の最大値,最小値を求める問題では, 頂点の座標 (軸から遠い側の)区間の端における二次関数の値;




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
このような式で表されるものが 2 2 次関数です。 中学では、 y = ax2 y = a x 2 を学習しました。 これは x x の 2 2 次関数の一部分を学習したということです。 b = c = 0 b = c = 0 の特殊ケースのみを学習最後に,2次関数と方程式,不等式の関係について学習します。2次方程式ax 2 bxc=0 の解の個数は,2次関数y=ax 2 bxc とx軸との共有点の個数に一致します。2次方程式の単元で学んだ「b 24ac」という式は,2次関数の単元でも活躍します。連立方程式を解いて2次関数を求める方法 これは簡単です! 3点を通る2次関数を求める場合は, y = a x 2 b x c とおく。 求める2次関数を y = a x 2 b x c とおく。 3点 ( 1, 8), ( − 2, 2), ( − 3, 4) を通るから, ① ② ③ { a b c = 8 ⋯ ⋯ ① 4 a − 2 b c = 2 ⋯ ⋯ ② 9 a − 3 b c = 4 ⋯ ⋯ ③ ② ① ② − ① より, 3 a − 3 b = − 6 a − b = − 2 ⋯ ⋯ ④ ③ ② ③ − ② より
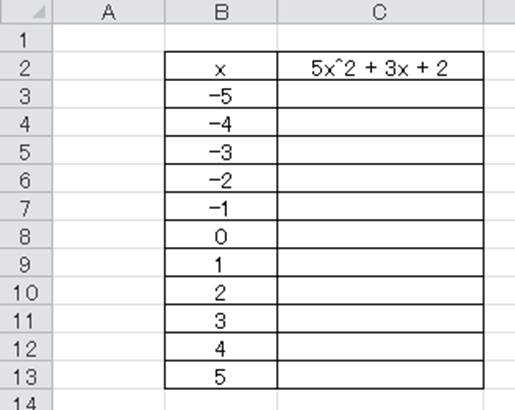



Excel エクセルで2次関数 2次方程式 のグラフを作成する方法




最高かつ最も包括的な2 次 関数 計算 最高のぬりえ
次の2次関数の最大値または最小値を求めよ (1)y=2x²4x1(ただし0≦x≦3) (2)y=x²4x(ただし4≦x≦1) ここでは、xの範囲が与えられた状態で2次関数の最大値・最小値を求める問題にチャレンジしていこう。



1



中学数学到達度テスト集中2前期 式の計算 連立方程式 1次関数 Gakurin1244 学林舎 通販 Yahoo ショッピング




中2の1次関数です 途中の計算過程まで書いてくれると助かります Clear



数学 中3 37 二次関数の変域 Youtube
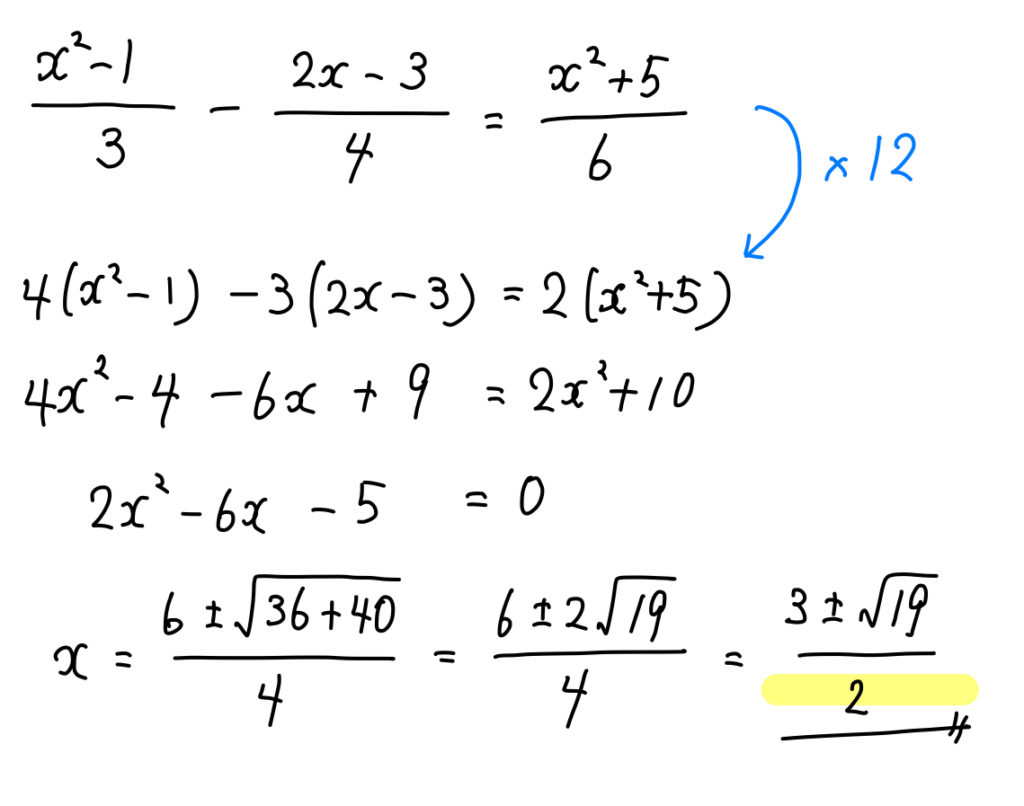



分数 小数 ルートを含む二次方程式の解き方まとめ 数スタ
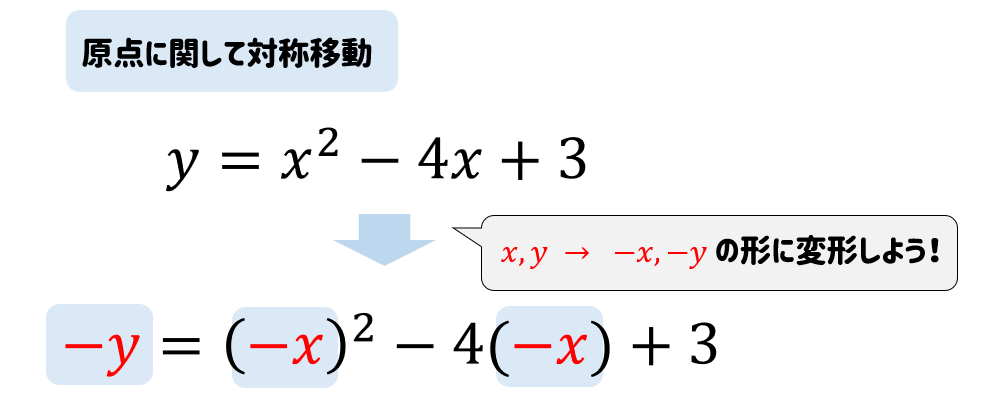



苦手な人向け 二次関数を対称移動したときの式の求め方を解説 数スタ
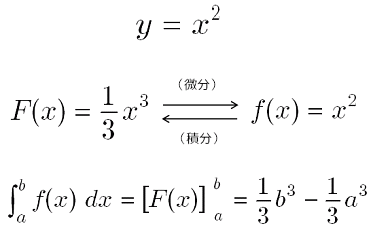



積分 区分求積を実際に計算する 二次関数の例 大人が学び直す数学




高校数学 二次関数の平方完成は難しくない 簡単に求めるやり方をわかりやすく解説 楽スタ



文字係数2次関数の頂点



エクセルのif関数を用いた条件分岐



Q Tbn And9gcqhtc24nuk7iqsfqrufuv8yena72hedeelrkw06jj3t Car0ms6 Usqp Cau




一次関数 2点を通る直線の式の求め方をイチから解説 Youtube




基本 絶対値のついた二次関数のグラフ なかけんの数学ノート




高校数学 数 39 2次関数 平方完成の練習編 Youtube



3




3次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ



ほのぼの数学頑張ろう 2次関数の最大 最小の問題 その2




数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo




中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
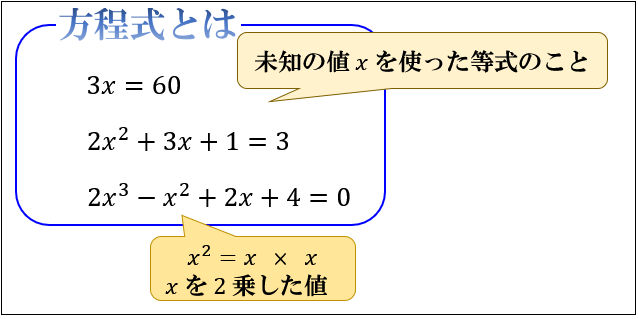



二次方程式の意味と解き方まとめ 解の公式 因数分解 アタリマエ
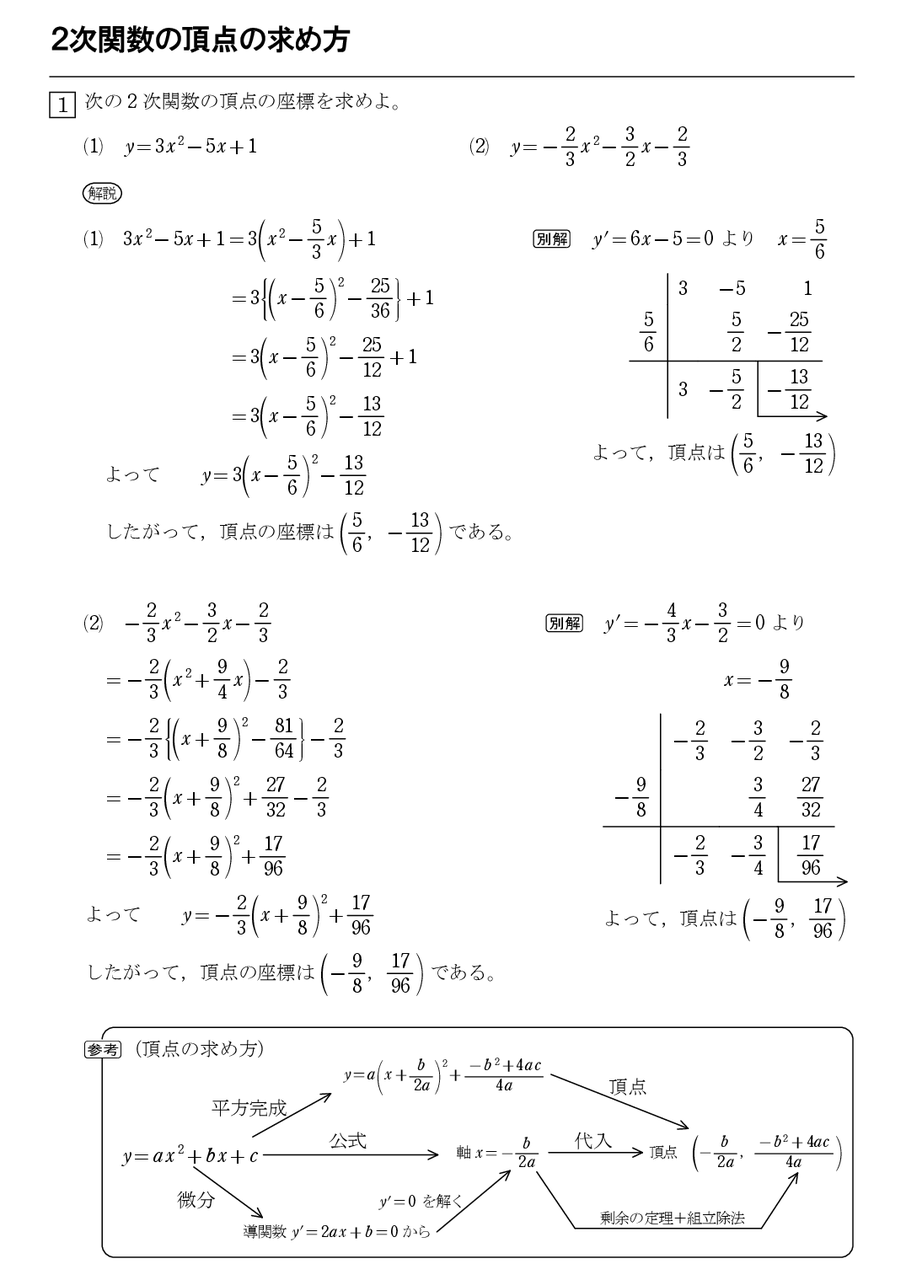



2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する
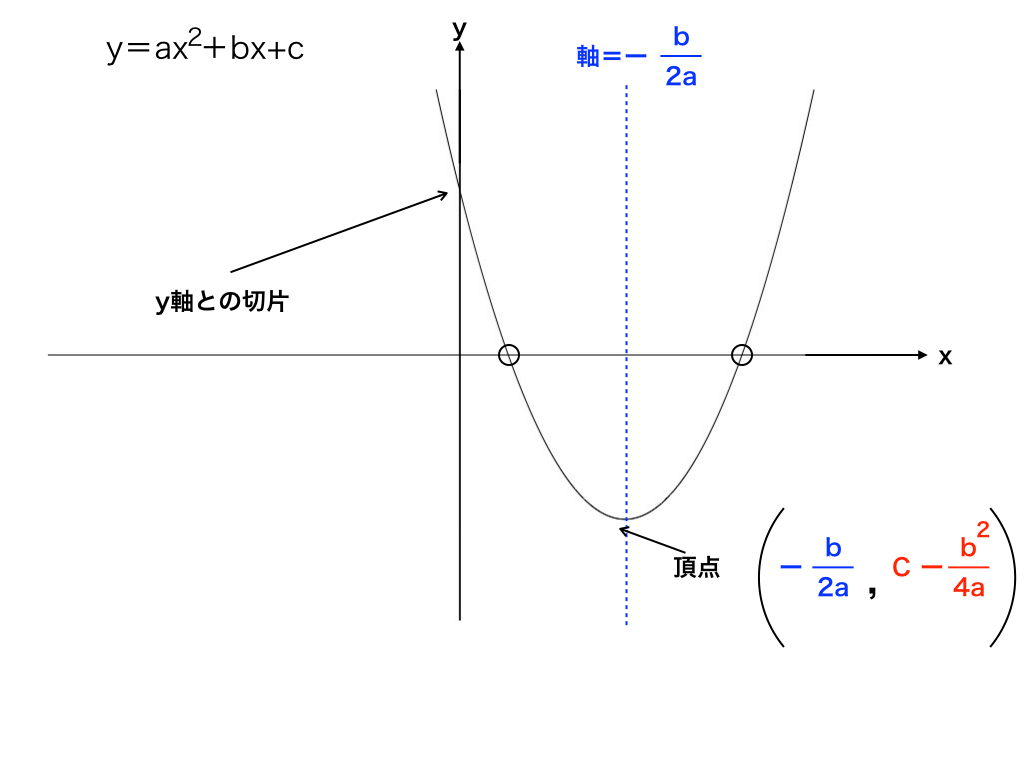



二次関数のグラフと解の存在範囲の問題をわかりやすく解説



2
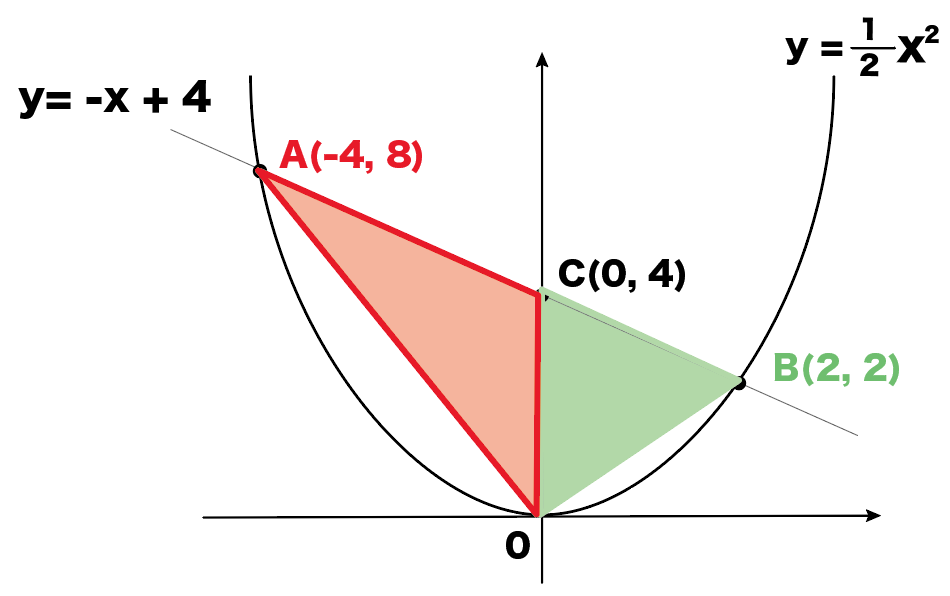



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく
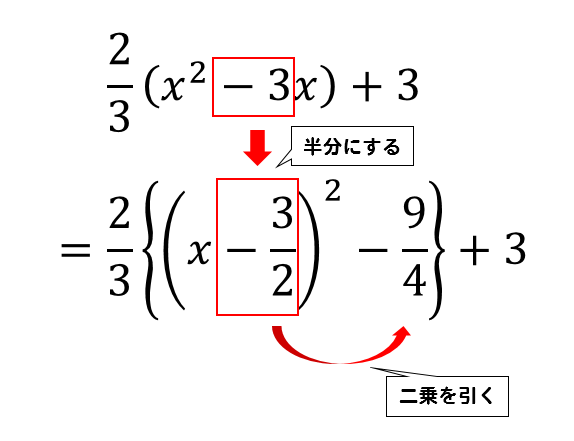



二次関数 頂点の求め方 公式は 問題を使ってイチから解説するぞ 数スタ




大学入試難問 化学解答 数学 2次関数 富岡市の総合学習塾 トータルアカデミー




二次方程式とは 見分け方が簡単にわかる中学レベルの問題 中学や高校の数学の計算問題



Lh3 Googleusercontent Com Proxy Sxewslo 5rstbisz Sm D7lorakfvpcb Yhb7fwidh5gngzimtvdepwr4xaymwjhhddjz84ruzjhe22qp V0k06 Ijonlv 5cudjnqmdpxwd7eydvyuasilkmj1x8xblrahezgwbaj9x06yku2v6hymzncc7xcnachxir2tqad7in6mrvu8lotkfnwt1hjg2euytqz4iawxfytt9g9uugles1yghnxctpj2suw4v0zgmsxdxvcsc8knj08eiw1zskkuylyziy3jsza9qoazilk4bgpb6vvpj5yvlbcfxsmj2mafjzrz8mgdhiler7a3bsxcvqprpphbbtky08oqdeqfxu04ktnde7b4




2次関数から2次方程式を考える 数学i フリー教材開発コミュニティ Ftext



ほのぼの数学頑張ろう 2次関数の決定の問題




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




三角関数講座その3 置き換え 2次関数 高校数学の知識庫




C言語 2次方程式を解く方法をご紹介します Takuya B Com




平方完成して二次関数のグラフを書く問題です 今グラフの 4を求めるのにy 0を平方完 Clear
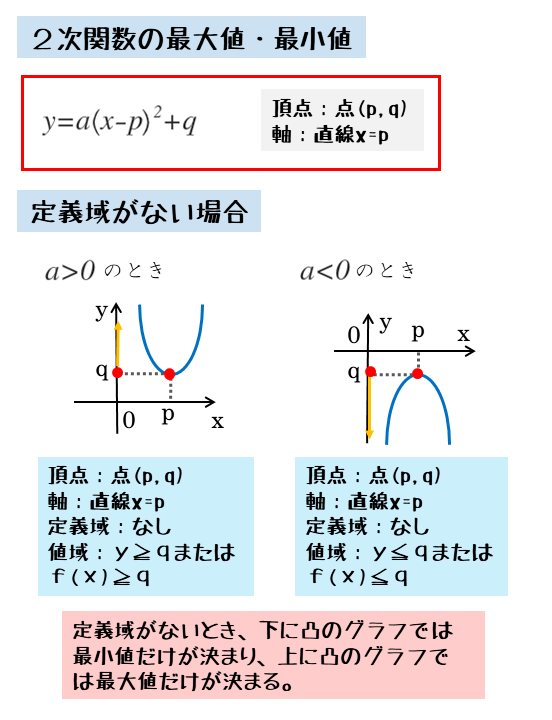



2次関数 2次関数の最大値や最小値について 日々是鍛錬 ひびこれたんれん
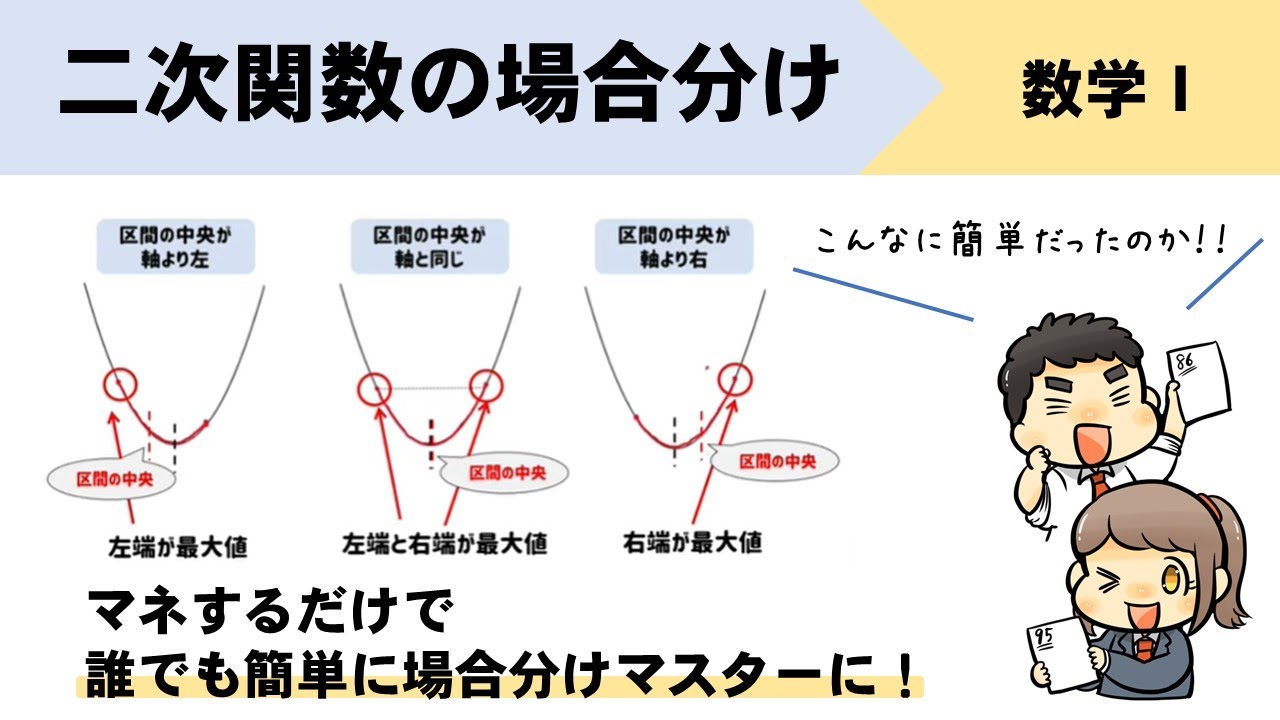



二次関数の場合分け 最大最小の応用問題の解き方をイチから解説 Youtube
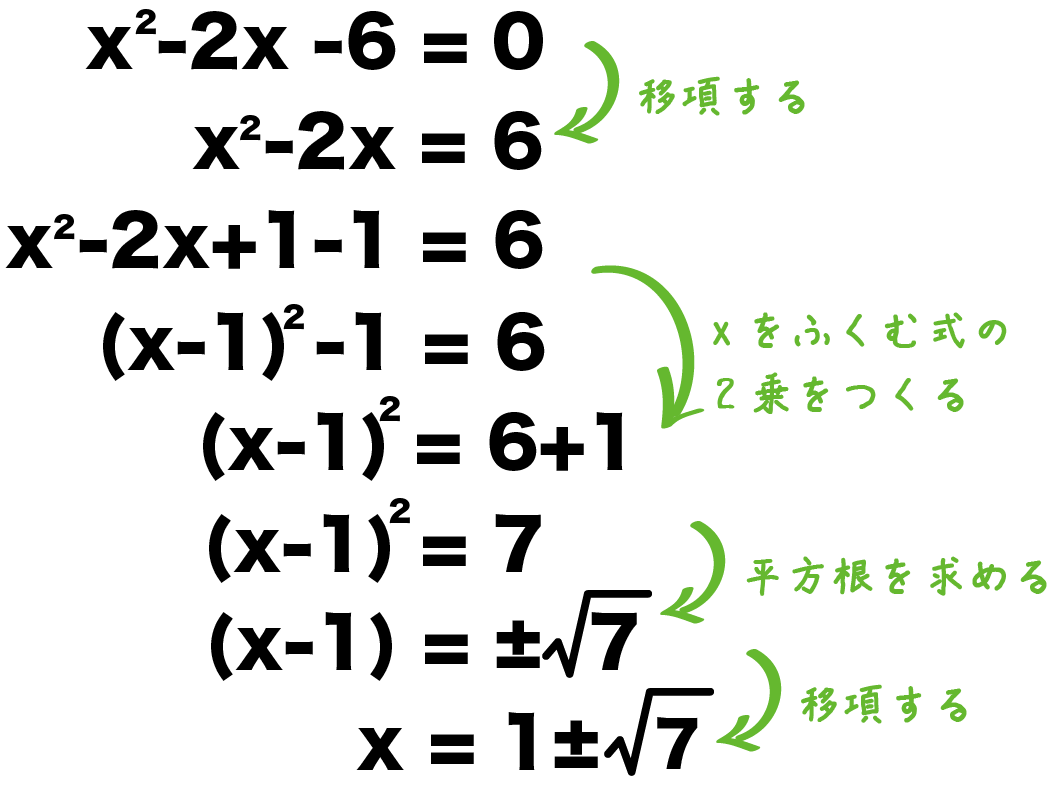



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく




二次方程式の解の公式 導き方 証明法を分かりやすく解説 アタリマエ




2次不等式と2次関数 数学i フリー教材開発コミュニティ Ftext




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月



1
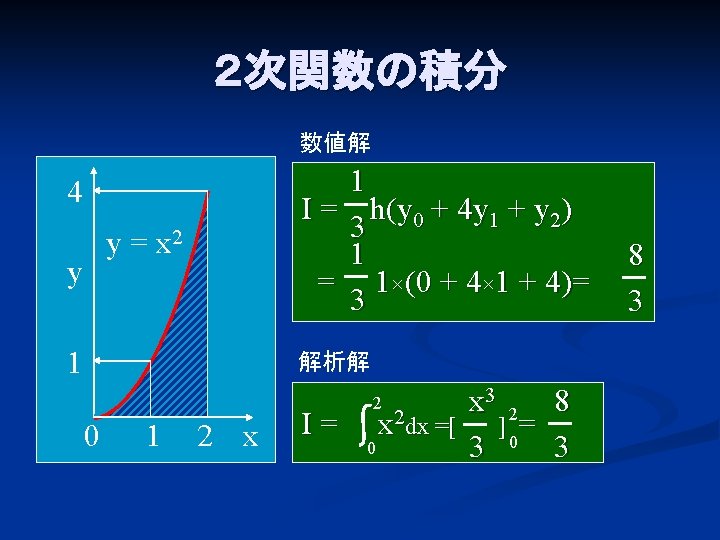



I 0 5h Y 0y 1y 1y 2
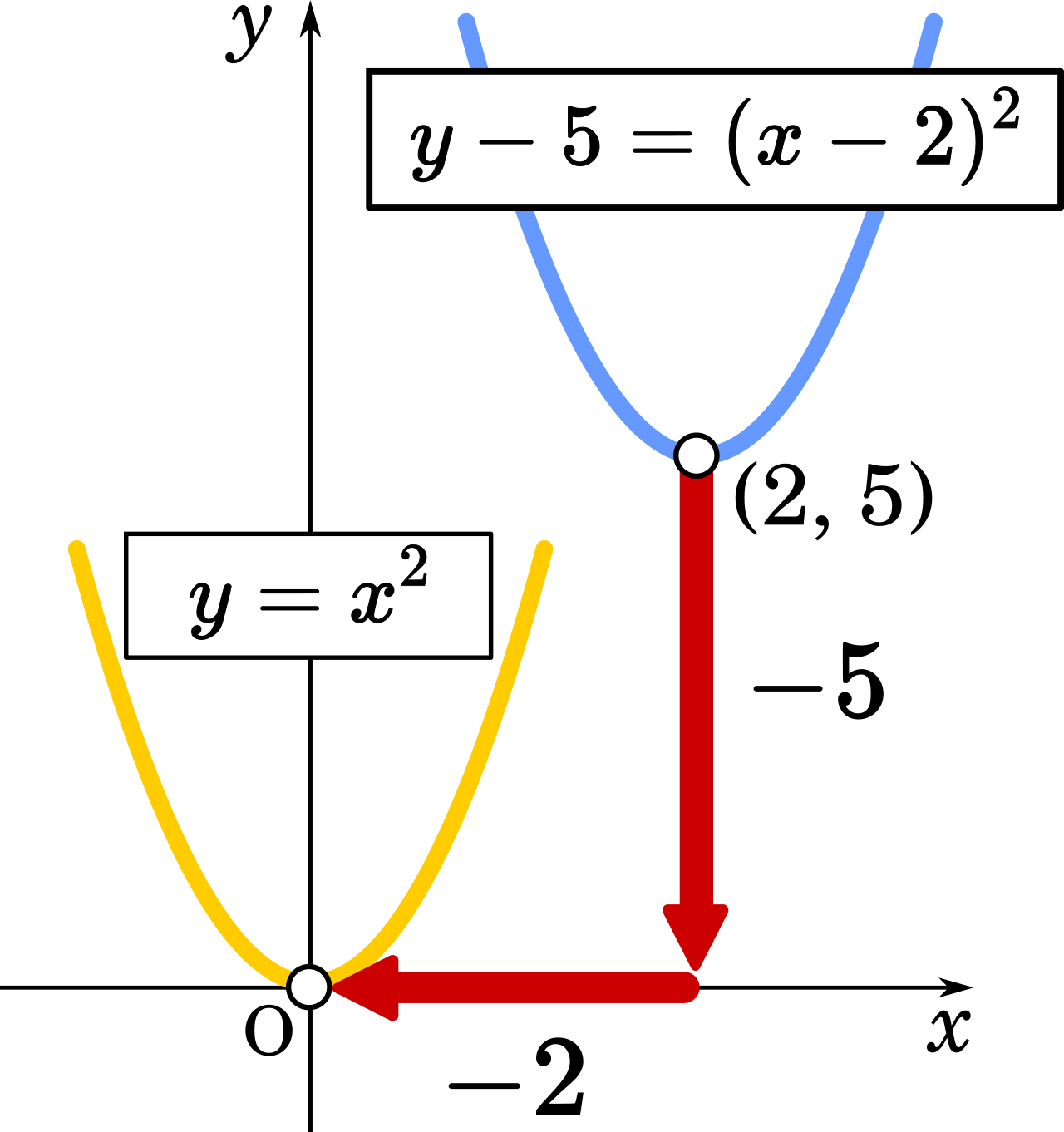



数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書




毎日計算練習問題 2次関数の頂点座標 彦根市の高校数学専門個別指導学習塾 安澤数学教室
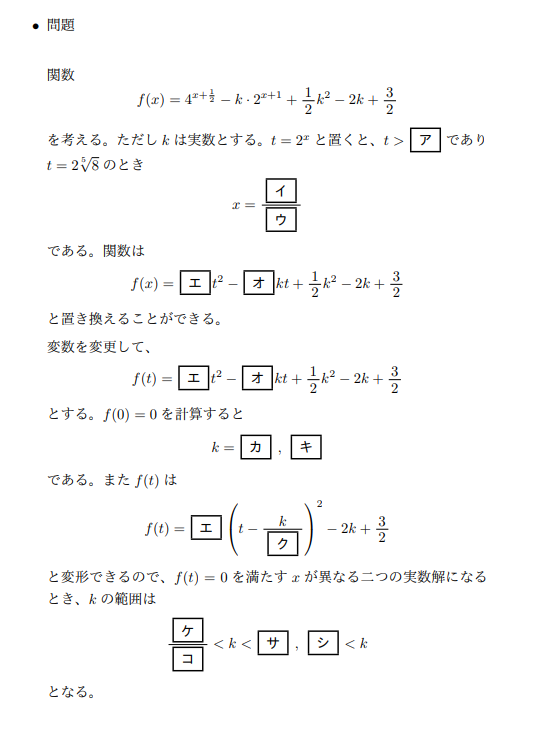



指数関数 対数関数講座その2 指数から二次関数へ 高校数学の知識庫




高校数 2次関数 頂点の求め方 オンライン無料塾 ターンナップ Youtube




不定積分と定積分の基本 定義と公式 Irohabook



二次関数とは 平方完成の公式や最大値 最小値 決定の問題 受験辞典



2次関数のグラフで分数のときはどう計算をして書くのですか 画像の Y Yahoo 知恵袋




2次関数 平方完成の手順について 数学 定期テスト対策サイト



文系微積分定積分公式 Of 京極一樹の数学塾会員頁



中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係



二次関数の移動




数学1a 二次関数の決定 です Clear



Lh3 Googleusercontent Com Proxy 99t7f Tyckdtkcr6m Mskicargahutcb0o70tnfeh0dwqcidvhzcuzzd0lcs9vvjeearbfsq9bprf6l7srfvae0u6vx6 D300a2iudubekfg3nyulxde6cebvytm14xrocamj Dkewdgje5eizoplpaqza2ciwn0wfqjtuj8wra6q8vphcelfpegdgzahcomzrbgqsov8wvz42jw Mn69ehfavqcttg Oldxhe4xrwq3wqua5cew3h8if9ytmvoqktztc7m Wag7xo30y0iuwvyy Dmkgbyuf 9zauxyay9ua6ss3mbqeriabjtqrw




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




高校数学 2元2次連立方程式3パターン 受験の月




中学数学 2次方程式の解の公式を導出する 平方完成 偏差値40プログラマー
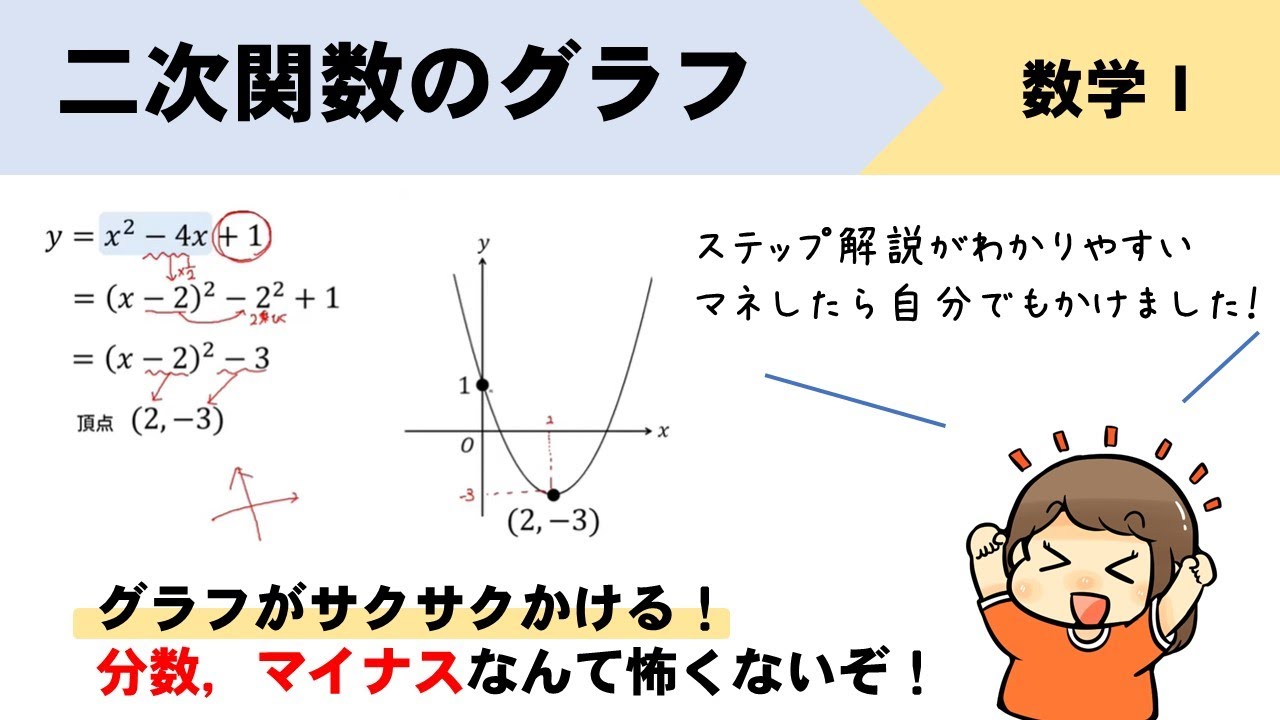



数学苦手な高校生向け 二次関数グラフの書き方を初めから解説 数スタ




2次関数4 直列計算で表を暗算する 怜悧玲瓏 高校数学を天空から俯瞰する




まなてぃ先生 鈴木真人 Twitterren 二次関数の平行移動と平方完成のまとめ スペースの関係で平行移動が結果論になってるのが悔やまれる リツイート歓迎です 数学 勉強 受験 ノート まとめ




超簡単 二次関数の頂点の求め方 平方完成と公式 2つを慶應生が解説してみた 練習問題付き 高校生向け受験応援メディア 受験のミカタ



二次関数のグラフの書き方と公式を使った最大値最小値問題の解き方 Studyplus スタディプラス
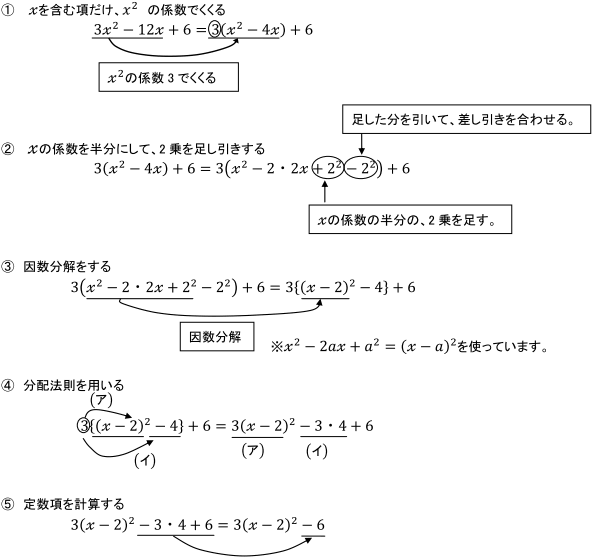



平方完成の手順について 数学 苦手解決q A 進研ゼミ高校講座
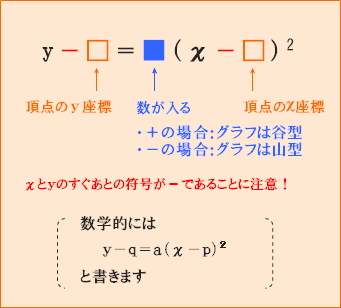



二次関数のグラフを選ぶ問題




数 2次関数 標準形の求め方 素早く頂点を求める手法の紹介 教えたい 人のための 数学講座




カッコの2乗がついた二次方程式の解き方 カッコを外したらこれをしよう 中学や高校の数学の計算問題
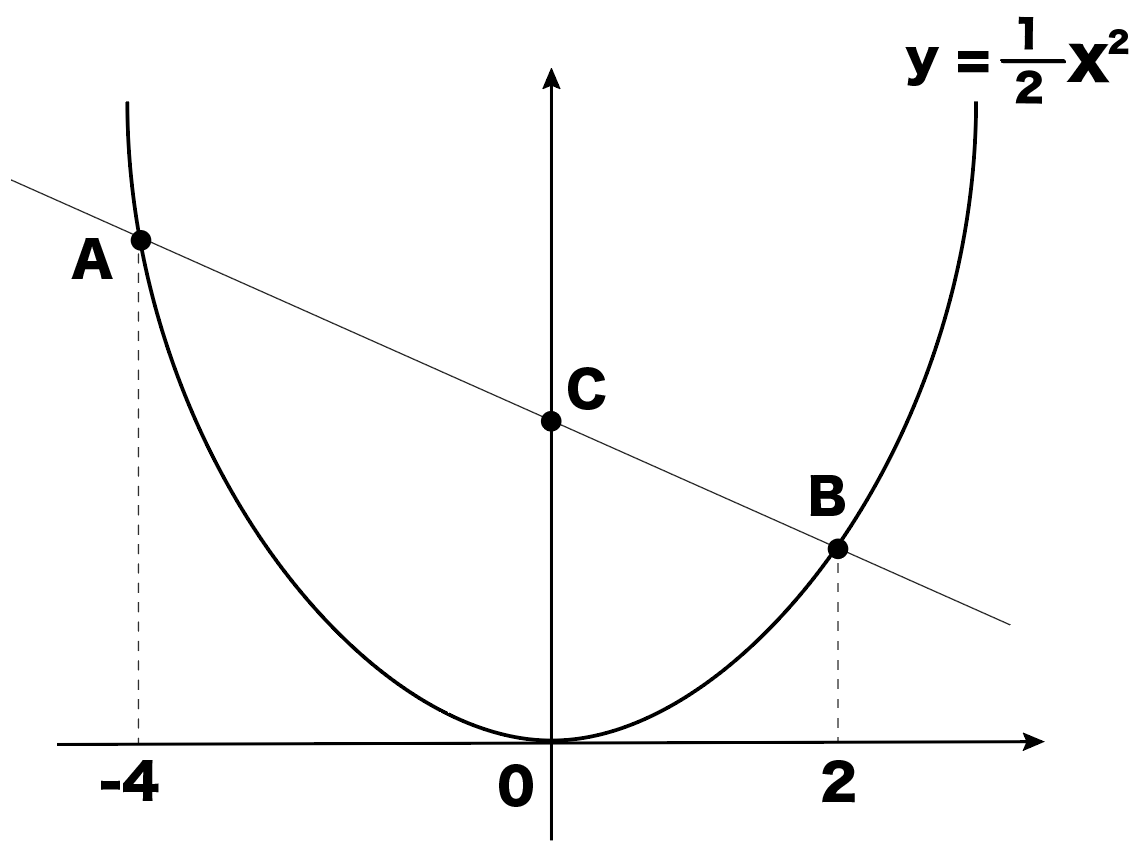



二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく
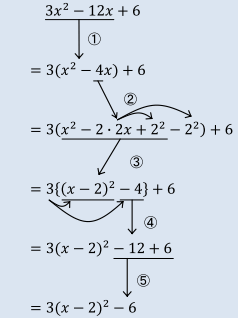



平方完成の手順について 数学 苦手解決q A 進研ゼミ高校講座




基本 2次関数の決定 数学苦手ですorz




二次関数の式と値の求め方 2 現役塾講師のわかりやすい中学数学の解き方




第3回 1次関数 2次関数とグラフ 例題8について
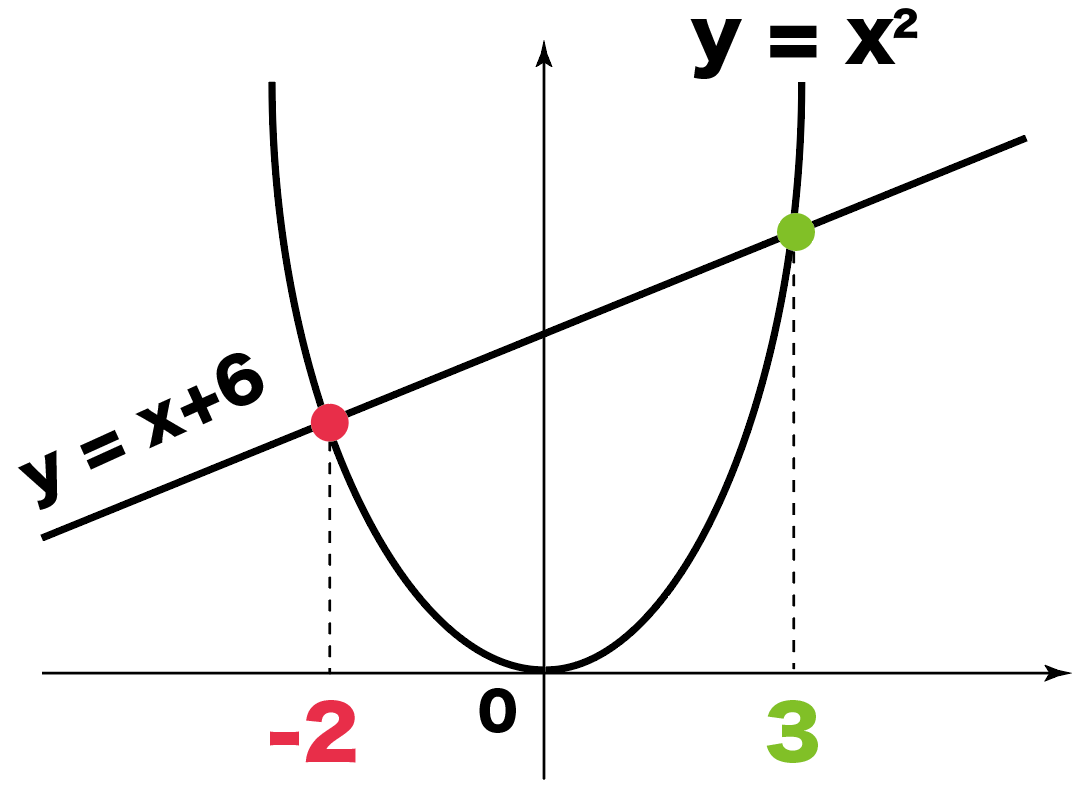



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



Lh3 Googleusercontent Com Proxy 7txni9x41xwiy0ga X Aq9eyx3mfwiptgqr6wihkgw3z0clgf7xrsj2jeewcmf98vsiqdp0snasy2ven0 Tdnkp61lt Srcyu0pcdp54mdjnnhwyfsmymrobdxmfxsd6wimisent Rsyxdd9odsyswhvo7thgvr8atxwcchlhlwncbp8stdbk 9fk3mebkngdtybugor0qvfpb Hq5et7znlwqjlo1aidhvto4nr63inbly0ivwe6p7ycat8x2wd7may1ufeyz1mazbqryjs9xesqp Hzgsfucrib1cawss5xcjwzts




平方完成の解き方 公式と計算問題 Irohabook




2次方程式と2次関数 数学i フリー教材開発コミュニティ Ftext




2 の青線の と の計算の途中式教えてください Clear




世界一わかりやすい数学問題集中3 4章 二次関数




二次方程式で解の公式を使う問題 見分け方は因数分解がポイント 中学や高校の数学の計算問題




数学i 2次関数の決定問題 Mike先生のstudyブログ
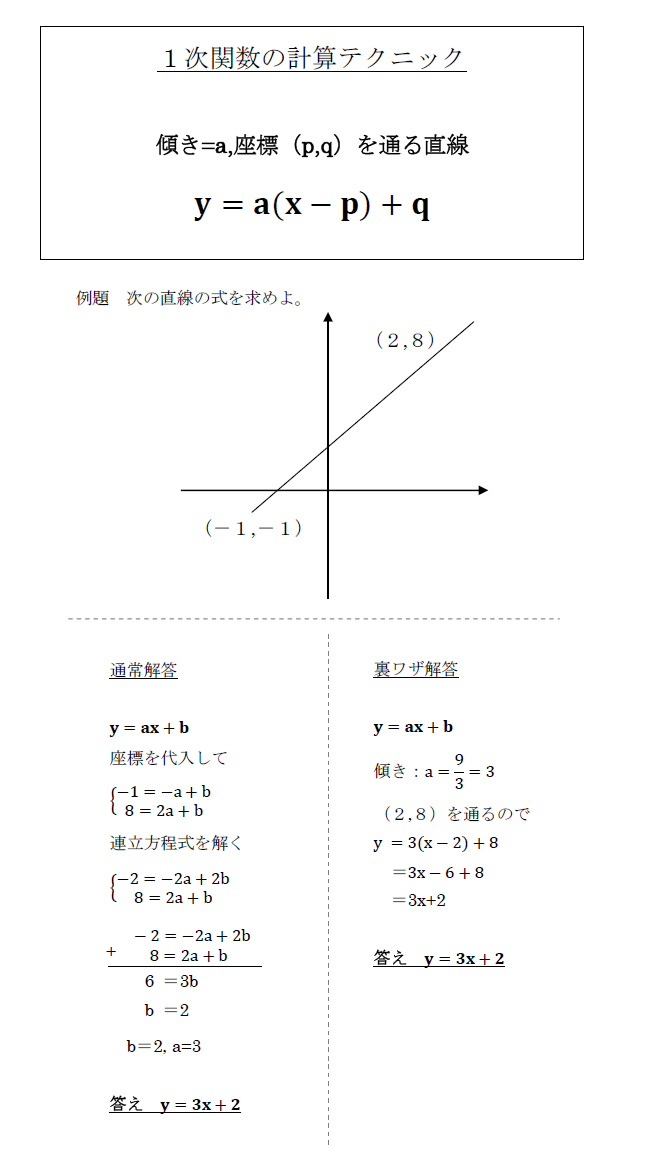



受験 定期試験 数学解き方集 裏技 解法 1次関数の計算テクニック 中学数学




高校数学 2次関数がx軸から切り取る線分の長さ 受験の月




標準 二次関数と微分 なかけんの数学ノート




Excel エクセルで2次関数 2次方程式 の計算を行う方法




逆関数とは 逆関数の求め方と逆関数の微分を基本から解説 高校生向け受験応援メディア 受験のミカタ



二次関数のグラフの書き方と 頂点 軸 切片の求め方 受験辞典



0 件のコメント:
コメントを投稿